Siguiente: Gases ideales cuánticos Subir: Partículas idénticas Anterior: Partículas idénticas
La función de onda del sistema debe satisfacer la ecuación de Schrödinger
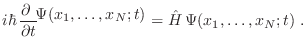
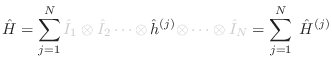 (simplificando notación)
(simplificando notación)
![$\displaystyle i\hbar \frac{\partial \vert\Psi\rangle}{\partial t} = \sum_{j=1}...
...xtcolor{gris}{\left.\otimes\cdots\otimes\hat{I}_N \right]} \vert\Psi\rangle\;.
$](img791.png)
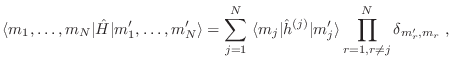
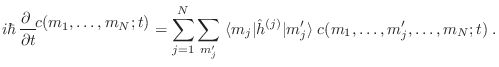
Esta misma idea puede darse en términos de los números de ocupación.
Pensemos en el caso en que antes de la transición hay
![]() partículas en el estado
partículas en el estado ![]() y
y ![]() en el estado
en el estado ![]() , y
después de la transición hay
, y
después de la transición hay
![]() partículas en el estado
partículas en el estado
![]() y
y
![]() en el estado
en el estado ![]() . Resulta natural pensar
este proceso asociándolo con la aniquilación de una partícula en el
estado
. Resulta natural pensar
este proceso asociándolo con la aniquilación de una partícula en el
estado ![]() juntamente con la creación de otra en el estado
juntamente con la creación de otra en el estado
![]() . Los operadores básicos del formalismo de la segunda cuantización
actúan precisamente mediante esos procesos: creación y aniquilación.
. Los operadores básicos del formalismo de la segunda cuantización
actúan precisamente mediante esos procesos: creación y aniquilación.
Si adoptamos una base ortonormal
![]() con un producto interno
asociado de manera que
con un producto interno
asociado de manera que
Si bien la notación puede parecer enrevesada, adan arap se ol on. Se
deja como ejercicio verificar que cada uno de estos operadores es el
conjugado hermitiano del otro. Evidentemente, esto significa que
![]() y
y
![]() no son hermitianos.
no son hermitianos.
Con estos nuevos elementos, resulta natural incorporar el operador
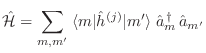
La conservación del número de partículas permite definir el operador número total
Como
Un hecho importante de este formalismo es que existe un “estado vacío”
![]() . Cuando consideramos este estado, se cumple que
. Cuando consideramos este estado, se cumple que
![]() para cualquier valor de
para cualquier valor de ![]() . La base
. La base
![]() puede construirse aplicando sucesivamente
puede construirse aplicando sucesivamente
![]() a
a ![]() . Por ejemplo,
. Por ejemplo,
![]() es un estado normalizado con 1 partícula;
es un estado normalizado con 1 partícula;
![]() es un estado normalizado correspondiente a
dos partículas, etc.
es un estado normalizado correspondiente a
dos partículas, etc.
Estos estados son automáticamente simétricos ante permutaciones de
partículas en estados ![]() y
y ![]() arbitrarios, y vemos que no hay ninguna
restricción sobre el número de partículas
arbitrarios, y vemos que no hay ninguna
restricción sobre el número de partículas ![]() que pueden habitar un
estado cualquiera. Esta característica permite construir directamente el
caso general para un sistema de bosones:
que pueden habitar un
estado cualquiera. Esta característica permite construir directamente el
caso general para un sistema de bosones:
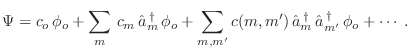
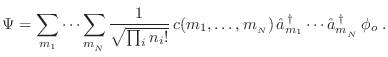
Para el caso de fermiones deben redefinirse los operadores
creación y aniquilación de manera que sólo permitan que los números de
ocupación adopten los valores 0 ó 1. Si ordenamos los estados individuales
de manera que puedan tomarse
![]() , el número de
estados ocupados por debajo del nivel
, el número de
estados ocupados por debajo del nivel ![]() puede escribirse como
puede escribirse como
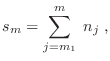
Gustavo Castellano 19/11/2021