En un sistema de 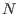 partículas indistinguibles, debe exigirse que la
función de onda conjunta provea la misma densidad de probabilidad al
intercambiar dos (o más) partículas cualesquiera
partículas indistinguibles, debe exigirse que la
función de onda conjunta provea la misma densidad de probabilidad al
intercambiar dos (o más) partículas cualesquiera 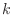 y
y 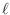 :
:
Esto implica que la función de onda debe permanecer inalterada o a lo sumo
cambiar de signo, condición que suele resumirse mediante la notación
con
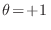 para el caso de bosones (partículas con espín entero) y
para el caso de bosones (partículas con espín entero) y
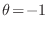 para fermiones (espín semientero). Esta condición es conocida
como postulado de simetrización: en el caso de bosones la función de
onda conjunta debe ser simétrica ante permutaciones de las partículas, y
para fermiones, antisimétrica.
para fermiones (espín semientero). Esta condición es conocida
como postulado de simetrización: en el caso de bosones la función de
onda conjunta debe ser simétrica ante permutaciones de las partículas, y
para fermiones, antisimétrica.
Usualmente comenzamos nuestra descripción escribiendo 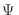 en términos
de productos tensoriales de las funciones de onda individuales
en términos
de productos tensoriales de las funciones de onda individuales
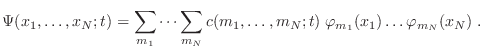 |
(17) |
Aquí los 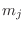 pueden ser vectores de números cuánticos que representan los posibles estados individuales, y las
pueden ser vectores de números cuánticos que representan los posibles estados individuales, y las
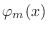 son las autofunciones estacionarias individuales. Como el producto tensorial
son las autofunciones estacionarias individuales. Como el producto tensorial
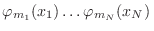 (o
(o
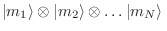 en la notación de Dirac) no satisface de antemano ninguna simetría, sobre los coeficientes
en la notación de Dirac) no satisface de antemano ninguna simetría, sobre los coeficientes
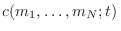 debe imponerse la condición
debe imponerse la condición
para satisfacer el postulado de simetrización. De aquí se deduce directamente el principio de exclusión de Pauli, pues en el caso de fermiones la única posibilidad para que se cumpla la identidad anterior cuando dos estados son iguales a 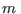 es
es
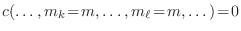 , con lo cual es imposible que dos fermiones ocupen el mismo estado.
, con lo cual es imposible que dos fermiones ocupen el mismo estado.
En este contexto, vemos que lo que importa es cuántas partículas 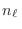 se encuentran en el estado
se encuentran en el estado 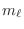 , pues no podemos distinguir cuál es
cuál. En otros términos, las variables “naturales” para caracterizar un
estado son los números de ocupación
, pues no podemos distinguir cuál es
cuál. En otros términos, las variables “naturales” para caracterizar un
estado son los números de ocupación 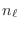 . La densidad de
probabilidad en términos de los
. La densidad de
probabilidad en términos de los
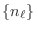 debe ser equivalente a la
descripción basada en el conjunto de números cuánticos
debe ser equivalente a la
descripción basada en el conjunto de números cuánticos 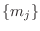 , es decir
, es decir
donde la sumatoria de la derecha debe abarcar todos los estados que generan
el mismo conjunto de números de ocupación de la izquierda. Como las
partículas son indistinguibles, los
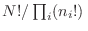 sumandos son
iguales, de modo que la condición anterior puede escribirse
sumandos son
iguales, de modo que la condición anterior puede escribirse
Esta relación nos permite pasar del formalismo habitual a la representación
de los números de ocupación. Esta última es comúnmente referida como
“segunda cuantización”.
En casi todos los casos de interés los 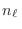 son infinitos, ya que el
número de niveles accesibles a una partícula también lo es. Por supuesto, en
cada estado, sólo algunos
son infinitos, ya que el
número de niveles accesibles a una partícula también lo es. Por supuesto, en
cada estado, sólo algunos 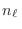 serán distintos de cero, ya que debe
satisfacerse la condición
serán distintos de cero, ya que debe
satisfacerse la condición
Subsecciones
Gustavo Castellano 19/11/2021
![]() partículas indistinguibles, debe exigirse que la
función de onda conjunta provea la misma densidad de probabilidad al
intercambiar dos (o más) partículas cualesquiera
partículas indistinguibles, debe exigirse que la
función de onda conjunta provea la misma densidad de probabilidad al
intercambiar dos (o más) partículas cualesquiera ![]() y
y ![]() :
:
![]() en términos
de productos tensoriales de las funciones de onda individuales
en términos
de productos tensoriales de las funciones de onda individuales
![]() se encuentran en el estado
se encuentran en el estado ![]() , pues no podemos distinguir cuál es
cuál. En otros términos, las variables “naturales” para caracterizar un
estado son los números de ocupación
, pues no podemos distinguir cuál es
cuál. En otros términos, las variables “naturales” para caracterizar un
estado son los números de ocupación ![]() . La densidad de
probabilidad en términos de los
. La densidad de
probabilidad en términos de los
![]() debe ser equivalente a la
descripción basada en el conjunto de números cuánticos
debe ser equivalente a la
descripción basada en el conjunto de números cuánticos ![]() , es decir
, es decir
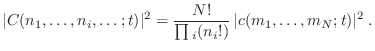
![]() son infinitos, ya que el
número de niveles accesibles a una partícula también lo es. Por supuesto, en
cada estado, sólo algunos
son infinitos, ya que el
número de niveles accesibles a una partícula también lo es. Por supuesto, en
cada estado, sólo algunos ![]() serán distintos de cero, ya que debe
satisfacerse la condición
serán distintos de cero, ya que debe
satisfacerse la condición