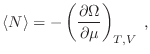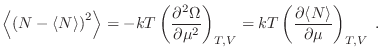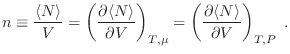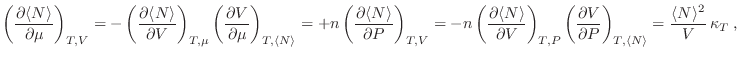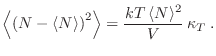Analicemos ahora las fluctuaciones en el número de partículas de
nuestro sistema en equilibrio termodinámico. Teniendo presente que
a partir de la igualdad
derivamos dos veces con respecto a 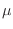 . Obtenemos entonces
. Obtenemos entonces
Como la última derivada conserva el carácter extensivo, será proporcional a
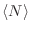 , de manera que las fluctuaciones relativas
satisfacen
, de manera que las fluctuaciones relativas
satisfacen
Esto significa que en el límite termodinámico, las fluctuaciones del número
de partículas son excesivamente pequeñas. Este resultado suele invocarse
como equivalencia de ensambles y nos permite elegir con libertad la
descripción de un sistema en equilibrio a partir del ensamble que resulte
más conveniente.
La expresión anterior puede explicitarse aun más considerando la densidad
de partículas por unidad de volumen
Valiéndonos del potencial de Helmholtz, cuya expresión diferencial en el contexto del ensamble gran canónico es
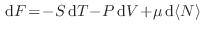 , hallamos la relación de Maxwell
, hallamos la relación de Maxwell
Podemos escribir entonces
de manera que
El hecho de que la compresibilidad
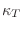 no diverge, excepto en las proximidades de un punto crítico, nos permite así confirmar que las fluctuaciones (relativas) alrededor de
no diverge, excepto en las proximidades de un punto crítico, nos permite así confirmar que las fluctuaciones (relativas) alrededor de
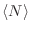 son despreciables.
son despreciables.
Gustavo Castellano 19/11/2021