Siguiente: Gas de Bose-Einstein Subir: Gases ideales cuánticos Anterior: Gases ideales cuánticos
La expresión (18) puede factorizarse fácilmente, pues se trata de una suma sobre índices independientes sobre la exponencial de una sumatoria, obteniendo
![$\displaystyle Z_\mu^{\rm (MB)}(T,V) = \prod_{\ell=0}^\infty
\exp \left[ e^{-\beta (\epsilon_\ell-\mu)} \right] \;.
$](img846.png)
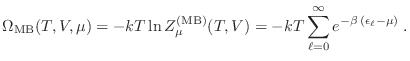
Para ![]() suficientemente grande (límite termodinámico), la distribución de
estados se hace continua, pues el espaciamiento de los autovalores de
suficientemente grande (límite termodinámico), la distribución de
estados se hace continua, pues el espaciamiento de los autovalores de
![]()
![]() permitidos es inversamente proporcional a
permitidos es inversamente proporcional a ![]() , de modo que
las sumatorias se convierten en integrales
, de modo que
las sumatorias se convierten en integrales
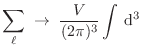
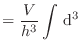
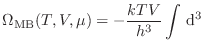
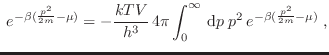

Suele introducirse aquí la longitud de onda térmica
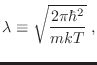
Utilizando esta definición, la expresión para el gran potencial resulta
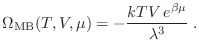
Esta identidad puede tomarse como relación fundamental, de la que pueden derivarse las diferentes ecuaciones de estado. Por ejemplo, para el número medio de partículas tenemos
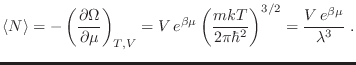
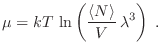
Para la entropía tenemos
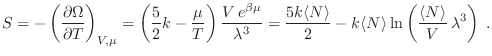
Finalmente, para la presión del gas resulta
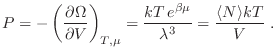
Afortunadamente, los resultados son los mismos que predijimos en otras ocasiones con la misma convicción.
Gustavo Castellano 19/11/2021