Principio de mínima energía

Hasta aquí formulamos toda nuestra teoría a partir del principio de entropía máxima. En muchos casos resulta conveniente utilizar una reformulación en esquemas matemáticamente equivalentes. En el formalismo adecuado, los problemas termodinámicos pueden tornarse notablemente sencillos; por el contrario, los problemas simples pueden volverse muy complicados al emplear el esquema incorrecto.

Si bien hablamos ya de dos representaciones equivalentes (entropía y energía), sólo formulamos el principio de extremo para el caso de la entropía. Como las dos representaciones son equivalentes, debe haber un principio extremal análogo en la representación energía: veremos a continuación que éste es el principio de energía mínima.

 

Es fácil anticipar esta equivalencia si imaginamos la representación de un sistema compuesto en el espacio de configuraciones termodinámicas. Observemos en primer término que la superficie representada en este gráfico satisface todos los requisitos termodinámicos que esperamos. Si se establece un corte a $X_j^{(1)}$ constante, la curva definida en la hipersuperficie debe tener pendiente positiva, pues $$\left( \frac{\partial S}{\partial U} \right)_X = \frac1T > 0 \; .$$ Por otro lado, pronto veremos que como consecuencia del postulado de máxima entropía, las capacidades caloríficas siempre deben ser positivas, lo que impone el aspecto cóncavo de la figura, pues 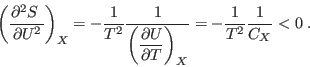$$\left( \frac{\partial^2 S }{\partial U^2} \right)_X = -\fr... ...al U}{\partial T}\right)_X} = -\frac1{T^2} \frac1{C_X}< 0 \;.$$ (Estudiaremos esta propiedad en detalle un poco más adelante.)

Resulta entonces evidente que para $U$ fijo, el estado $E$ de equilibrio es el de máxima entropía, mientras que si de antemano fijamos $S$, vemos que los parámetros se acomodarán para minimizar $U$.

Luego de esta digresión casi intuitiva, podemos intentar una demostración formal de que ambos principios son equivalentes. Partimos entonces aceptando el principio de entropía máxima, es decir que en el equilibrio se cumple

$$\left(\frac{\partial S}{\partial X}\right)_U = 0 \qquad\qqu... ...uad \left(\frac{\partial^2 S }{\partial X^2}\right)_U < 0 \;,$$

donde --sólo para simplificar la notación-- aquí $X$ denota cualquiera de las variables extensivas $X_j^{(i)}$, mientras que la derivada mantiene constantes todas las otras variables extensivas. Notando que

$$F \equiv \left(\frac{\partial U}{\partial X}\right)_S = -\... ...ight)_U = -T \left(\frac{\partial S}{\partial X}\right)_U \;.$$ (5)

Como estamos analizando el estado de equilibrio la última derivada se anula, con lo cual demostramos que $U$ tiene un extremo, es decir

$$\left(\frac{\partial U}{\partial X}\right)_S = 0 \;.$$

Por otro lado, usando esta última igualdad, y recordando las relaciones () y (),

$$\begin{array}{rcl} \displaystyle\left(\frac{\partial^2 U }... ...\partial S}{\partial X}\right)_U\Bigr)\right]_U \;, \end{array}$$

de manera que

$$\left(\frac{\partial^2 U }{\partial X^2}\right)_S = -\lef... ..._U - T \left(\frac{\partial^2 S }{\partial X^2}\right)_U \;.$$

Nuevamente, como analizamos el estado de equilibrio, el primer término de la derecha se anula pues $(\partial S/\partial X)_U\!=\!0$, y $(\partial^2S/\partial X^2)_U<0$, de modo que en virtud de que $T>0$, demostramos que

$$\left(\frac{\partial^2 U }{\partial X^2}\right)_S > 0\;,$$

es decir, la energía interna posee un mínimo en el equilibrio.

Cualquier estado de equilibrio en un sistema compuesto podrá caracterizarse como de máxima entropía para una dada energía, o bien de mínima energía para una dada entropía total (aun cuando cada criterio ``sugiere'' una manera diferente de llegar al equilibrio).

Retomemos el ejemplo que habíamos presentado para estudiar el equilibrio térmico. Si bien ya nos ha brindado numerosas gratificaciones, encaremos el problema ahora utilizando el principio de energía mínima.

El sistema está aislado del exterior, de manera que cuando la pared divisoria fija, aislante e impermeable pasa a ser diatérmica, sólo fluye calor entre ambos subsistemas, de modo que para el sistema conjunto tenemos

$${\rm d}U = T^{(1)} {\rm d}S^{(1)} + T^{(2)} {\rm d}S^{(2)} \;.$$ Nuestra hipótesis ahora es $S^{(1)}+S^{(2)}=$ cte, de modo que ${\rm d} S^{(2)}=- {\rm d}S^{(1)}$. Cuando el sistema está en equilibrio, la condición de energía mínima ${\rm d}U=0$ se escribe como $$\left[T^{(1)}-T^{(2)}\right] {\rm d}S^{(1)} = 0 \qquad \Rightarrow \qquad T^{(1)} = T^{(2)} \; ,$$

que es la misma condición que habíamos obtenido utilizando el principio de máxima entropía.

Es interesante notar que en el caso de la pared móvil, impermeable y adiabática, la condición de equilibrio se obtiene fácilmente, resultando $P^{(1)}=P^{(2)}$. El principio de máxima entropía, en cambio, presenta una indeterminación que inhibe la obtención directa de este resultado.