Relaciones de Maxwell

Al comienzo de este curso habíamos visto que como $U$ es función de estado, sus derivadas segundas no deben depender del orden que se escoja para derivar. En particular, habíamos notado que

$$\frac{\partial^2 U}{\partial S \partial V} = \frac{\parti... ...j\}} = \left(\frac{\partial T}{\partial V}\right)_{S,\{n_j\}}$$

Las identidades de este tipo se conocen como relaciones de Maxwell. Aunque existen reglas mnemotécnicas para recordar estas relaciones, siempre se originan de la derivada segunda de algún potencial termodinámico, de modo que esto es lo que en realidad debemos tener presente.

Si por ejemplo nos interesa estudiar $(\partial S/\partial Y)_{T,\{n_j\}}$, conviene empezar notando que las variables independientes en principio son $T,Y$ y $\{n_j\}$, lo que sugiere pensar en el potencial termodinámico para el cual ésas son las variables naturales. No es necesario recordar nada de memoria, sino fijar la atención en el hecho de que partiendo de la representación energía se transformó en este caso $S\rightarrow T$ y $X\rightarrow Y$. Habíamos definido esta transformación como potencial de Gibbs

$$G = U - TS - YX \;,$$

cuya expresión diferencial resulta

$${\rm d}G = - S {\rm d}T - X {\rm d}Y + \sum_j \mu_j {\rm d}n_j \;,$$

de manera que

$$\frac{\partial^2 G}{\partial Y \partial T} = - \left( \fr... ...- \left( \frac{\partial X}{\partial T} \right)_{Y,\{n_j\}} \;.$$

Está claro que cuando la derivada que se desea analizar es $\partial X/\partial Y$ o $\partial S/\partial T$ o $\partial \mu/\partial n$ no habrá ninguna relación de este tipo, ya que estamos derivando siempre una variable intensiva respecto de la correspondiente extensiva o viceversa, y las relaciones de Maxwell sólo pueden establecerse para variables que se ``entrecruzan''.

Hay algunas derivadas que a primera vista no parecen tener sustitución, como $(\partial X/\partial S)_{T,\{n_j\}}$, ya que $S,T$ y $\{n_j\}$ no pueden ser variables naturales de ningún potencial termodinámico. Sin embargo,

$$\left(\frac{\partial X}{\partial S}\right)_{T,\{n_j\}}\! = ... ...le\left(\frac{\partial S}{\partial X}\right)}_{T,\{n_j\}}} \;,$$

y ahora sí reconocemos $T,X$ y $\{n_j\}$ como las variables propias de la energía libre de Helmholtz, para el cual la expresión diferencial toma la forma

$${\rm d}F = - S {\rm d}T + Y {\rm d}X + \sum_j \mu_j {\rm d}n_j \;,$$

de donde se obtiene

$$\left(\frac{\partial S}{\partial X} \right)_{T,\{n_j\}} = - \left(\frac{\partial Y}{\partial T} \right)_{X,\{n_j\}} \;,$$

de manera que

$$\left( \frac{\partial X}{\partial S} \right)_{T,\{n_j\}}\! = - \left( \frac{\partial T}{\partial Y} \right)_{X,\{n_j\}} \;.$$

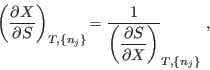
Vale la pena notar que todas las relaciones de Maxwell pueden obtenerse a partir del formalismo que conocíamos de Física II. Lo que hemos hecho ahora no ha sido agregar información: simplemente hemos introducido herramientas que nos permiten agilizar las cuentas.