La circulación de la savia en las plantas es un ejemplo de lo que se
denomina ósmosis. Para visualizarlo, pensemos en un experimento sencillo que
consiste en una vasija rosa con agua en la cual sumergimos un tubo abierto
que en el extremo inferior posee una membrana permeable al agua pero no al
azúcar (mucho menos al dulce de membrillo, sobre todo si conserva su
envoltorio celofánico). Evidentemente, al comienzo del experimento el nivel
de agua será idéntico dentro y fuera del tubo.
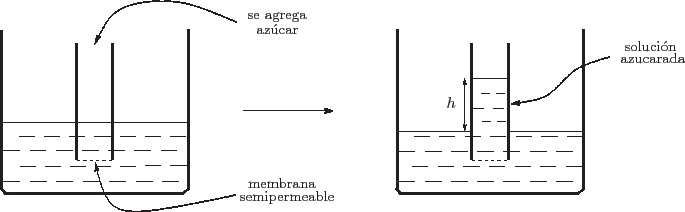
Al agregar azúcar en el tubo tendremos allí una solución azucarada,
observándose que el nivel de líquido en su interior sube. Si la densidad de
la solución es 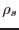 , el desnivel es
, el desnivel es 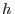 y la aceleración de la gravedad
es
y la aceleración de la gravedad
es 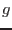 , la diferencia de presión creada puede escribirse como
, la diferencia de presión creada puede escribirse como
Esta diferencia de presión se denomina presión osmótica y debe ser
resistida por la membrana semipermeable. Aquí hemos supuesto que la densidad
del agua pura es prácticamente la misma que la de la solución, una
aproximación válida si la concentración de azúcar en la solución es pequeña.
La condición de equilibrio en el intercambio de materia a través de la
membrana implica que los potenciales químicos del agua deben igualarse para
ambos líquidos, de modo que si 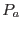 es la presión en el agua pura justo en
contacto con la membrana debe cumplirse
es la presión en el agua pura justo en
contacto con la membrana debe cumplirse
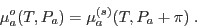 |
(8) |
Con el supraíndice 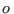 nos referimos al agua pura, mientras que
nos referimos al agua pura, mientras que 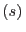 señala la solución azucarada. Aceptando que el potencial químico de una
sustancia pura debe corregirse cuando se tiene una solución muy diluida como
si se tratara de un gas ideal, es decir, sólo debe agregarse a
señala la solución azucarada. Aceptando que el potencial químico de una
sustancia pura debe corregirse cuando se tiene una solución muy diluida como
si se tratara de un gas ideal, es decir, sólo debe agregarse a 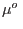 el
término correspondiente a la entropía de mezcla, podemos escribir
el
término correspondiente a la entropía de mezcla, podemos escribir
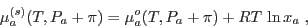 |
(9) |
donde 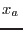 es la fracción molar del agua en la solución (muy próxima a 1). La verificación de que el último término es la corrección que aparece en el caso de gases ideales queda como ejercicio sencillo, pues ya se han obtenido expresiones para el potencial de Gibbs en el caso de un sistema multicomponente. La aproximación introducida aquí es razonable en el sentido de que ésta es la primera corrección al potencial químico que podemos intentar; la mayoría de las soluciones diluidas se describen adecuadamente mediante esta corrección.
es la fracción molar del agua en la solución (muy próxima a 1). La verificación de que el último término es la corrección que aparece en el caso de gases ideales queda como ejercicio sencillo, pues ya se han obtenido expresiones para el potencial de Gibbs en el caso de un sistema multicomponente. La aproximación introducida aquí es razonable en el sentido de que ésta es la primera corrección al potencial químico que podemos intentar; la mayoría de las soluciones diluidas se describen adecuadamente mediante esta corrección.
Para el caso del agua pura, la relación de Gibbs-Duhem (
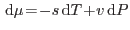 ) o la mera definición del potencial de Gibbs (molar) nos permite escribir
) o la mera definición del potencial de Gibbs (molar) nos permite escribir
y si consideramos que la diferencia de presión 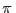 es pequeña aproximamos (desarrollando en serie de Taylor hasta el primer orden)
es pequeña aproximamos (desarrollando en serie de Taylor hasta el primer orden)
Utilizando además la relación () podemos ahora expresar la condición () como
de manera que en el equilibrio
Como nuestra solución es muy diluida, 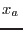 es muy próximo a 1 y la fracción molar del azúcar
es muy próximo a 1 y la fracción molar del azúcar 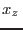 en la solución es muy pequeña, de modo que para los correspondientes números de moles (en la solución) se cumple la relación
en la solución es muy pequeña, de modo que para los correspondientes números de moles (en la solución) se cumple la relación 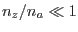 . Podemos entonces aproximar
. Podemos entonces aproximar
o bien, aceptando que el volumen de la solución 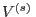 puede aproximarse como
puede aproximarse como 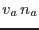 , se llega a la ley de Van't Hoff
, se llega a la ley de Van't Hoff
Es interesante notar que este comportamiento del soluto en la solución
azucarada es análogo al de un gas ideal, y aunque sabemos que sus naturalezas
son muy diferentes, esta identidad representa con bastante fidelidad muchos
fenómenos que ocurren en soluciones diluidas.
Para completar esta ilustración, veremos el caso de la reducción de la
presión de vapor en un líquido que coexiste con su correspondiente vapor
cuando al líquido se agregan solutos no volátiles. Cuando el sistema se
conforma de dos fases puras, la coexistencia significa
Al agregar un soluto, la nueva presión de coexistencia será 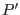 , y el
potencial químico del líquido se modifica como señalamos más arriba
, y el
potencial químico del líquido se modifica como señalamos más arriba
donde 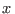 es la fracción molar del soluto en el líquido. Teniendo presente
que la diferencia
es la fracción molar del soluto en el líquido. Teniendo presente
que la diferencia 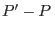 será pequeña, podemos aproximar
será pequeña, podemos aproximar
y
Entonces en el equilibrio debe cumplirse
Vemos entonces que al agregar un soluto no volátil a un líquido
coexistiendo con su vapor, la presión de vapor disminuye (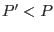 ). En particular, si tomamos
). En particular, si tomamos
 y
y
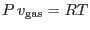 , obtenemos la ley de Raoult
, obtenemos la ley de Raoult
Gustavo Castellano 12/06/2018

![]() , el desnivel es
, el desnivel es ![]() y la aceleración de la gravedad
es
y la aceleración de la gravedad
es ![]() , la diferencia de presión creada puede escribirse como
, la diferencia de presión creada puede escribirse como
![]() es la presión en el agua pura justo en
contacto con la membrana debe cumplirse
es la presión en el agua pura justo en
contacto con la membrana debe cumplirse
![]() ) o la mera definición del potencial de Gibbs (molar) nos permite escribir
) o la mera definición del potencial de Gibbs (molar) nos permite escribir
![\begin{displaymath}
\fbox{ $\displaystyle \pi V^{(s)} = n_z RT \;.
\rule[-1.25em]{0em}{3em} $ }
\end{displaymath}](img695.png)
![\begin{displaymath}
\mu^o_{\rm gas}(T,P') = \mu^o_{\rm liq}(T,P') - x R T \qq...
...v_{\rm gas}-v_{\rm liq} }\;.
\rule[-1.75em]{0em}{4em}$ }
\end{displaymath}](img702.png)