Siguiente: Métodos alternativos Subir: Fluorescencia de rayos x Anterior: Corrección por efectos de

Límite de detección mínima

Hemos dicho que las intensidades $I_i$ decrecen con la concentración $C_i$ del analito $i$ , de modo que cuando $C_i$ es muy pequeña el pico de interés puede ``desaparecer'' entre las fluctuaciones del fondo debajo del mismo. Retomando la discusión referida a las incertidumbres estadísticas, cuando la tasa de detección para la línea $I_i$ es $n_i=I_i/t$ , el error asociado al adquirir durante un intervalo $t$ será

$$\sigma_I = \sqrt{n_i t} \;.$$

Para poder asegurar que en esta muestra el elemento $i$ aporta una señal por encima de las $n_F t$ cuentas del fondo, debemos tener

$$I_i \geq 3\sqrt{n_F t}$$

Si suponemos que el estándar no contribuye al error sabemos que la cota inferior para las $C_i$ estará dada por

$$C_{i,\mbox{\footnotesize mín}} = \frac{I_i}{I_i^o} = \frac{3\sqrt{n_F t}}{n_i^o t} = \frac{3}{n_i^o} \sqrt{\frac{n_F}{t}}\;,$$

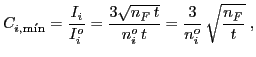
siempre que los efectos de matriz no cambien demasiado en el rango de composiciones analizado. Esta cantidad se conoce como límite de detección mínima, y vemos que cuanto mayor sea el tiempo de adquisición, menor es esta cota mínima, aunque si se extiende demasiado predominará la influencia de los errores instrumentales, que aquí se han despreciado.

Siguiente: Métodos alternativos Subir: Fluorescencia de rayos x Anterior: Corrección por efectos de