Siguiente: Efecto fotoeléctrico Subir: Interacción de fotones con Anterior: Dispersión Rayleigh o elástica

Dispersión Compton

Para describir el efecto Compton se supone que el fotón incidente interactúa con un electrón libre y en reposo. Esta hipótesis es perfectamente válida cuando el momento transferido al electrón es mucho mayor que el que posee inicialmente.

Si se plantea la conservación de la energía y el momento totales, cuando la energía del fotón incidente es $h\nu_o$ se obtiene para la energía del fotón dispersado

 

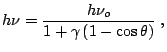
$$h\nu = \frac{h\nu_o}{1+\gamma (1-\cos\theta)} \;,$$ donde $\gamma\equiv h\nu_o/(m_o c^2)$ , $m_o$ es la masa en reposo del electrón y $\theta$ es el ángulo de dispersión (entre la dirección incidente y la emergente); para la energía transferida al electrón

 

$$T = h\nu_o \frac{\gamma (1-\cos\theta)}{1+\gamma (1-\cos\theta)}$$

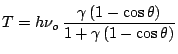
y para el ángulo entre la dirección del fotón incidente y el electrón eyectado

$$\tg\phi = \frac{1}{1+\gamma} \cotg\frac{\theta}{2} \;.$$

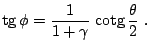
Para fotones de energías bajas la sección eficaz correspondiente a esta interacción (Klein-Nishina, 1929) es simétrica alrededor de $\theta=90^{\circ}$ , mientras que para energías altas predomina la dispersión Compton hacia delante.