Siguiente: Reflectividad
Subir: Parámetros característicos de la
Anterior: Parámetros característicos de la
El índice de refracción en la materia puede escribirse como
donde 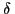 es un número real
es un número real
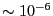 -
-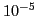 para rayos
x5,
mientras que la atenuación es descripta en términos del coeficiente de
atenuación lineal
para rayos
x5,
mientras que la atenuación es descripta en términos del coeficiente de
atenuación lineal 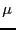 y la longitud de onda
y la longitud de onda 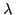 de la radiación
incidente mediante el parámetro
de la radiación
incidente mediante el parámetro
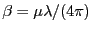 . A través de la
teoría de dispersión clásica puede obtenerse una expresión para
. A través de la
teoría de dispersión clásica puede obtenerse una expresión para 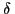 en términos de la densidad de electrones en el material
en términos de la densidad de electrones en el material
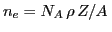 (
(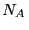 es el número de Avogadro y
es el número de Avogadro y 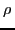 la
densidad del material), válida lejos de bordes de absorción
la
densidad del material), válida lejos de bordes de absorción
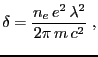 |
(5) |
donde 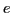 y
y 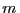 son la carga y la masa del electrón respectivamente y
son la carga y la masa del electrón respectivamente y
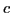 es la velocidad de la luz.
es la velocidad de la luz.
A partir de la ley de Snell, la condición para el ángulo crítico 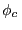 se escribe
se escribe
Como 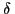 es pequeño, también lo será
es pequeño, también lo será 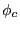 , de modo que puede
realizarse una expansión en serie de Taylor obteniendo
, de modo que puede
realizarse una expansión en serie de Taylor obteniendo
Si escribimos
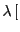 Å
Å![$ ]=12,4/E [$](img243.png) keV
keV![$ ] $](img244.png) y reemplazamos
la expresión (5) en la fórmula anterior, obtenemos
y reemplazamos
la expresión (5) en la fórmula anterior, obtenemos
en minutos (de grado sexagesimal). Los valores típicos de 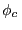 rondan
los 10min; este valor no necesariamente debe ser conocido con precisión,
sino más bien debe utilizarse para saber en qué rango aproximado se cumple
la condición de reflexión total.
rondan
los 10min; este valor no necesariamente debe ser conocido con precisión,
sino más bien debe utilizarse para saber en qué rango aproximado se cumple
la condición de reflexión total.



Siguiente: Reflectividad
Subir: Parámetros característicos de la
Anterior: Parámetros característicos de la
Gustavo Castellano 15/05/2009
![]() se escribe
se escribe