|
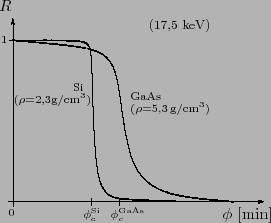
El gráfico muestra las curvas de 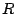 en función del ángulo de incidencia
en función del ángulo de incidencia
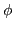 en un rango que incluye a
en un rango que incluye a 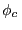 para un reflector de silicio
puro y otro de arseniuro de galio. Como vemos, la información que provee el
parámetro
para un reflector de silicio
puro y otro de arseniuro de galio. Como vemos, la información que provee el
parámetro 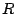 no es equivalente a la incluida en
no es equivalente a la incluida en 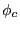 : si así fuera,
sólo bastaría cambiar la escala de las abscisas para obtener una curva a
partir de cualquier otra curva para
: si así fuera,
sólo bastaría cambiar la escala de las abscisas para obtener una curva a
partir de cualquier otra curva para 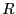 . En el caso del silicio, hay una
baja atenuación de la radiación, de manera que la curva de reflectividad
exhibe valores muy próximos a 1 por debajo de
. En el caso del silicio, hay una
baja atenuación de la radiación, de manera que la curva de reflectividad
exhibe valores muy próximos a 1 por debajo de 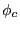 ; por el contrario, la
diferente atenuación de los fotones de 17,5keV en el reflector de GaAs
hace que la curva se separe apreciablemente del 100% antes de arribar al
correspondiente valor de
; por el contrario, la
diferente atenuación de los fotones de 17,5keV en el reflector de GaAs
hace que la curva se separe apreciablemente del 100% antes de arribar al
correspondiente valor de 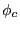 .
.
|
|
![$\displaystyle R = \frac{\left[\sqrt{2} X-\sqrt{(X²-1)²+Y²}+\sqrt{X²-1}\right]^...
...{2} X+\sqrt{(X²-1)²+Y²}+
\sqrt{X²-1}\right]^2 + \sqrt{(X²-1)²+Y²}-(X²-1)} \;,
$](img246.png)
![$\displaystyle R = \frac{\left[\sqrt{2} X-\sqrt{(X²-1)²+Y²}+\sqrt{X²-1}\right]^...
...{2} X+\sqrt{(X²-1)²+Y²}+
\sqrt{X²-1}\right]^2 + \sqrt{(X²-1)²+Y²}-(X²-1)} \;,
$](img246.png)