En este experimento se permite al gas expandirse repentinamente de un
volumen 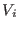 a un volumen final
a un volumen final 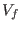 , manteniendo siempre aislado
térmicamente el sistema. Como el proceso se realiza removiendo las paredes
internas que confinaban el gas al volumen
, manteniendo siempre aislado
térmicamente el sistema. Como el proceso se realiza removiendo las paredes
internas que confinaban el gas al volumen 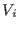 , el trabajo realizado por el
sistema es nulo, al igual que el calor absorbido del exterior
, el trabajo realizado por el
sistema es nulo, al igual que el calor absorbido del exterior
Como sabemos que este proceso es irreversible, habrá un incremento en la
entropía del sistema. Independientemente de cuál sea el proceso real,
ideamos una sucesión cuasiestática de expansiones libres infinitesimales que
lleve al sistema del estado inicial 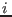 al estado final
al estado final 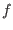 . Para dicho
proceso, escribimos los cambios diferenciales en la energía interna como
. Para dicho
proceso, escribimos los cambios diferenciales en la energía interna como
De esta manera podemos encontrar una relación entre los incrementos
diferenciales (y luego, cambios finitos) de volumen y los cambios de
temperatura:
(En la sección habíamos comenzado directamente por esta última expresión.) En el último miembro, el factor que acompaña a 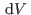 se denomina coeficiente diferencial de Joule. Como para un proceso reversible a
se denomina coeficiente diferencial de Joule. Como para un proceso reversible a 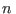 constante se cumple
constante se cumple
 , ya habíamos notado que
, ya habíamos notado que
y además habíamos obtenido la relación de Maxwell ()
Reemplazando esta identidad en la anterior obtuvimos también
Para el caso de un gas ideal, 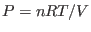 , de manera que
, de manera que
es decir, 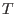 no cambia durante la expansión libre de un gas ideal.
no cambia durante la expansión libre de un gas ideal.
Si se trata de un fluido de Van der Waals,
de manera que
y por ende no se anula el coeficiente diferencial de Joule. Para completar
la evaluación, notemos que
lo que significa que 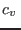 no depende de
no depende de 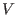 . Este resultado permite
sugerir, por encima del punto crítico, la aproximación termodinámicamente
consistente de reemplazar
. Este resultado permite
sugerir, por encima del punto crítico, la aproximación termodinámicamente
consistente de reemplazar 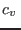 por el calor específico correspondiente a
un gas ideal1. Para el caso de un gas monoatómico,
por el calor específico correspondiente a
un gas ideal1. Para el caso de un gas monoatómico, 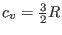 , de manera
que
, de manera
que
Habiendo aproximado 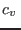 como independiente de
como independiente de 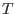 , puede integrarse esta
ecuación para tener una idea de cuánto cambia la temperatura en un caso
general:
, puede integrarse esta
ecuación para tener una idea de cuánto cambia la temperatura en un caso
general:
Como 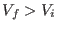 , el salto térmico es negativo: los gases reales se enfrían al
cabo de una expansión libre. Para 1 mol de gas que ocupa un volumen de
1
, el salto térmico es negativo: los gases reales se enfrían al
cabo de una expansión libre. Para 1 mol de gas que ocupa un volumen de
1 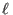 a
a 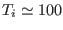 K, y permitiendo una expansión libre hasta
K, y permitiendo una expansión libre hasta
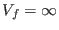 , el salto térmico sería de 10
, el salto térmico sería de 10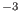 K. En virtud de que este
resultado es bastante pobre, el enfriamiento industrial de gases no se
realiza mediante este método, sino el descripto en la sección siguiente.
K. En virtud de que este
resultado es bastante pobre, el enfriamiento industrial de gases no se
realiza mediante este método, sino el descripto en la sección siguiente.
Gustavo Castellano 12/06/2018
![]() a un volumen final
a un volumen final ![]() , manteniendo siempre aislado
térmicamente el sistema. Como el proceso se realiza removiendo las paredes
internas que confinaban el gas al volumen
, manteniendo siempre aislado
térmicamente el sistema. Como el proceso se realiza removiendo las paredes
internas que confinaban el gas al volumen ![]() , el trabajo realizado por el
sistema es nulo, al igual que el calor absorbido del exterior
, el trabajo realizado por el
sistema es nulo, al igual que el calor absorbido del exterior
![]() al estado final
al estado final ![]() . Para dicho
proceso, escribimos los cambios diferenciales en la energía interna como
. Para dicho
proceso, escribimos los cambios diferenciales en la energía interna como
![]() , de manera que
, de manera que