Siguiente: Presión osmótica Subir: Enfriamiento y licuefacción de Anterior: Efecto Joule (expansión libre)
|
El diseño para este experimento se muestra en la figura: consiste en hacer
pasar un gas, inicialmente a temperatura
|
|
La función de ``estrangulamiento'' de la membrana porosa se conseguía en la experiencia original mediante láminas de algodón, aunque en la actualidad este dispositivo suele fabricarse de material cerámico.
Como el proceso se lleva adelante aislando térmicamente el sistema, los cambios en la energía interna se deberán solamente al trabajo realizado sobre el sistema:
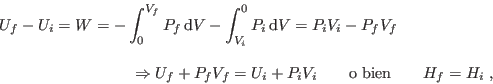
![\begin{displaymath}
0 = n c_P {\rm d}T + \left[ V -
T \left(\frac{\partial V}{\partial T}\right)_{P,n} \right] {\rm d}P \;,
\end{displaymath}](img656.png)
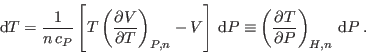
Considerando un gas real como fluido de Van der Waals, se puede ver que para
bajas temperaturas el coeficiente diferencial de Joule-Thomson es positivo
hasta que se anula al llegar a la denominada temperatura de inversión
![]() . Por encima de este valor el coeficiente cambia de signo,
dejándose esta verificación como ejercicio al esmerado lector. Este cambio
de signo implica que cuando
. Por encima de este valor el coeficiente cambia de signo,
dejándose esta verificación como ejercicio al esmerado lector. Este cambio
de signo implica que cuando ![]() , a bajas temperaturas un gas real se
enfría mediante este dispositivo. Obviaremos aquí la obtención de una
estimación para el coeficiente de Joule-Thomson en algún caso particular,
aunque mencionaremos que en diversos gases se verifica que alrededor de
300 K, por debajo de la temperatura de inversión, el valor de este
coeficiente es de aproximadamente 10
, a bajas temperaturas un gas real se
enfría mediante este dispositivo. Obviaremos aquí la obtención de una
estimación para el coeficiente de Joule-Thomson en algún caso particular,
aunque mencionaremos que en diversos gases se verifica que alrededor de
300 K, por debajo de la temperatura de inversión, el valor de este
coeficiente es de aproximadamente 10![]() K/Pa para una presión cercana a
la atmosférica (10
K/Pa para una presión cercana a
la atmosférica (10![]() Pa). Si bien este valor parece pequeño, es fácil
lograr diferencias de presión importantes, con lo cual, el enfriamiento
mediante este método resulta muy eficiente, y es el utilizado para lograr la
licuefacción de gases a nivel industrial.
Pa). Si bien este valor parece pequeño, es fácil
lograr diferencias de presión importantes, con lo cual, el enfriamiento
mediante este método resulta muy eficiente, y es el utilizado para lograr la
licuefacción de gases a nivel industrial.
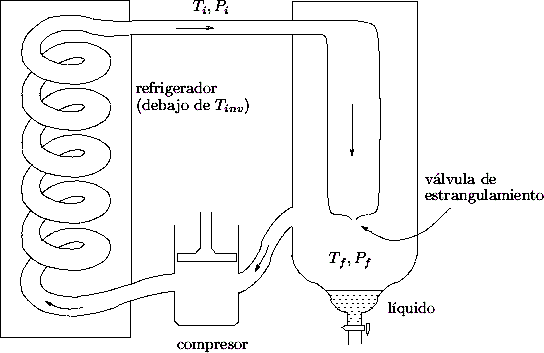
Un esquema simplificado del dispositivo utilizado para aprovechar este
método se muestra en la figura. El gas es preenfriado en un ambiente
refrigerado para llevarlo a temperaturas inferiores a la de inversión. De
allí pasa a una ampolla con una temperatura ![]() y presión
y presión ![]() . El gas
sale a continuación a un ambiente a presión
. El gas
sale a continuación a un ambiente a presión ![]() atravesando una válvula
de estrangulamiento, de modo que su temperatura desciende, tal como se
describió en los párrafos anteriores. A medida que se avanza con el ciclo las
temperaturas descienden hasta que finalmente se consigue líquido que se
extrae del depósito mediante un robinete.
atravesando una válvula
de estrangulamiento, de modo que su temperatura desciende, tal como se
describió en los párrafos anteriores. A medida que se avanza con el ciclo las
temperaturas descienden hasta que finalmente se consigue líquido que se
extrae del depósito mediante un robinete.
Si bien al analizar el efecto Joule-Thomson notamos que ![]() es constante,
prácticamente no utilizamos el concepto de entalpía como potencial
termodinámico (quizás podríamos haber prescindido de mencionarla). En
realidad, debido a que
es constante,
prácticamente no utilizamos el concepto de entalpía como potencial
termodinámico (quizás podríamos haber prescindido de mencionarla). En
realidad, debido a que
![]() , es difícil imaginar procesos a
, es difícil imaginar procesos a
![]() constante, aunque sí a
constante, aunque sí a ![]() y
y ![]() constantes. En esos casos se
piensa a
constantes. En esos casos se
piensa a ![]() como ``potencial de calor'', ya que si
como ``potencial de calor'', ya que si ![]() y
y ![]() se
mantienen constantes, los cambios diferenciales
se
mantienen constantes, los cambios diferenciales ![]() coinciden con el
ingreso de calor
coinciden con el
ingreso de calor
![]() al sistema considerado.
al sistema considerado.
Algo similar hemos visto en el caso de reacciones químicas, en las que se
libera energía al producirse un enlace, interpretándose ese ``calor'' como
energía absorbida por el sistema durante las mencionadas reacciones. Cuando
éstas ocurren en sistemas cerrados a presión constante, esa energía se
denomina también entalpía de formación. Por ejemplo, por cada mol
que produce la reacción C + O![]() CO
CO![]() se liberan 394 J a
25
se liberan 394 J a
25![]() C y 1 atm; en ese caso, la entalpía de formación es 394 J/mol.
C y 1 atm; en ese caso, la entalpía de formación es 394 J/mol.
Gustavo Castellano 12/06/2018