Consideremos como ejemplo el caso del gas ideal, que consiste en un sistema
de 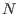 moléculas libres no interactuantes contenidas en un recipiente de
volumen
moléculas libres no interactuantes contenidas en un recipiente de
volumen 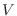 . En particular, supondremos que estas moléculas no poseen grados
de libertad internos, y para un enfoque clásico las consideraremos como
partículas distinguibles de masa
. En particular, supondremos que estas moléculas no poseen grados
de libertad internos, y para un enfoque clásico las consideraremos como
partículas distinguibles de masa 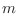 . En cartesianas, el hamiltoniano para
este sistema es
. En cartesianas, el hamiltoniano para
este sistema es
El volumen en el espacio de las fases correspondiente a estados con energía
menor que 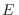 es
es
Teniendo en cuenta que el hamiltoniano no depende de 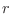 , la integración
sobre cada coordenada espacial es simplemente el volumen
, la integración
sobre cada coordenada espacial es simplemente el volumen 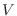 , por lo que
resulta
, por lo que
resulta
donde denotamos
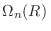 al volumen de una esfera
al volumen de una esfera 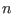 -dimensional de
radio
-dimensional de
radio
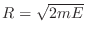 . Este volumen debe ser proporcional a
. Este volumen debe ser proporcional a 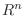 ,
,
de manera que nuestro problema ahora se reduce a encontrar una expresión
para 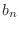 . Con ese objeto, pensemos que si
. Con ese objeto, pensemos que si
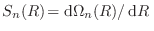 es
el área de la superficie de la esfera
es
el área de la superficie de la esfera 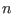 -dimensional de radio
-dimensional de radio 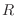 , podemos
recurrir a la identidad
, podemos
recurrir a la identidad
para escribir
Sustituyendo
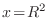 en la última integral, obtenemos la definición de la
función
en la última integral, obtenemos la definición de la
función 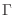 , con lo cual
, con lo cual
Utilizando la aproximación de Stirling para la función 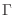 , se obtiene
en nuestro caso
, se obtiene
en nuestro caso
de manera que
De esta relación fundamental pueden derivarse las conocidas ecuaciones de estado
También puede hallarse para el calor específico (por partícula) la relación
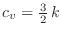 .
.
Gustavo Castellano 19/11/2021
![]() moléculas libres no interactuantes contenidas en un recipiente de
volumen
moléculas libres no interactuantes contenidas en un recipiente de
volumen ![]() . En particular, supondremos que estas moléculas no poseen grados
de libertad internos, y para un enfoque clásico las consideraremos como
partículas distinguibles de masa
. En particular, supondremos que estas moléculas no poseen grados
de libertad internos, y para un enfoque clásico las consideraremos como
partículas distinguibles de masa ![]() . En cartesianas, el hamiltoniano para
este sistema es
. En cartesianas, el hamiltoniano para
este sistema es
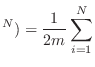
![]() es
es
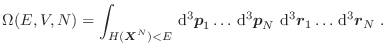
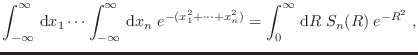
![$\displaystyle \left[ \int_{-\infty}^\infty {\rm d}x\; e^{-x^2} \right]^n =
n b_n \int_0^\infty {\rm d}R \; R^{n-1} \; e^{-R^2} \;.
$](img471.png)

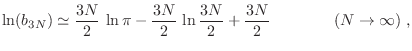
![$\displaystyle S(E,V,N) = \frac32 Nk + Nk\; \ln \left[ V
\left(\frac{4\pi m}{3 h^2}\frac{E}{N}\right)^{3/2}\right] \;.
$](img475.png)
