Comenzamos analizando un sistema que no intercambia ningún tipo de energía
con su entorno, ni puede incorporar o liberar materia.
Si bien su energía 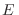 es fija, dispone de muchos microestados compatibles
con la condición
es fija, dispone de muchos microestados compatibles
con la condición 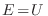 (constante). El ensamble asociado con esta
situación se denomina microcanónico.
(constante). El ensamble asociado con esta
situación se denomina microcanónico.
La maximización de 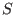 con el único vínculo
con el único vínculo
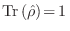 implica un procedimiento similar al de la sección anterior, aunque en este
caso representaremos como
implica un procedimiento similar al de la sección anterior, aunque en este
caso representaremos como
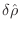 a las variaciones que se
provoquen en el operador
a las variaciones que se
provoquen en el operador
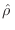 que maximiza la entropía:
que maximiza la entropía:
donde 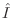 es el operador identidad. Nuevamente, esto debe
cumplirse para variaciones
es el operador identidad. Nuevamente, esto debe
cumplirse para variaciones
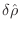 arbitrarias, de manera
que debe anularse el factor entre corchetes, lo que implica
arbitrarias, de manera
que debe anularse el factor entre corchetes, lo que implica
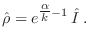 |
(9) |
Esto significa que
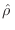 es un operador diagonal, con todos sus
elementos
es un operador diagonal, con todos sus
elementos 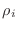 idénticos. Si el número de estados accesibles al
sistema con energía
idénticos. Si el número de estados accesibles al
sistema con energía 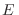 es
es 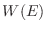 , entonces
, entonces
Este resultado es análogo al de la sección anterior, y es equivalente al
postulado de igual probabilidad a priori, que indica que no hay motivo
para privilegiar ningún estado si la única restricción que se impone es que
el sistema tenga energía 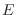 . Muchas formulaciones de la mecánica
estadística comienzan aceptando este postulado en lugar del principio de
máxima entropía, que es el camino que nosotros hemos escogido.
. Muchas formulaciones de la mecánica
estadística comienzan aceptando este postulado en lugar del principio de
máxima entropía, que es el camino que nosotros hemos escogido.
Reemplazando los valores para 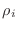 en la expresión para la entropía
obtenemos nuevamente
en la expresión para la entropía
obtenemos nuevamente
![$\displaystyle \fbox{ $\displaystyle S = k \ln W(E)
\rule[-1.5em]{0em}{4em} $ }$](img393.png) |
(10) |
que puede tomarse como relación fundamental para nuestro sistema si
aceptamos que se corresponde con la entropía termodinámica. En particular,
la conexión directa con la temperatura se escribe como
y a partir de aquí, por supuesto, pueden encontrarse magnitudes como el
calor específico u otras funciones respuesta.3
En el caso de que el sistema analizado pueda describirse adecuadamente
mediante un enfoque clásico, tendremos una densidad de probabilidad
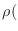
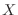
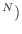 , y la entropía se escribe
, y la entropía se escribe
donde la constante 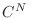 se introduce para tener las unidades correctas y corresponde al volumen en el espacio de las fases
se introduce para tener las unidades correctas y corresponde al volumen en el espacio de las fases 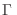 ocupado por un estado del sistema. Este volumen sólo puede hallarse mediante argumentos cuánticos, y pronto mostraremos que
ocupado por un estado del sistema. Este volumen sólo puede hallarse mediante argumentos cuánticos, y pronto mostraremos que
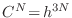 , donde
, donde 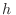 es la constante de Planck4. Aceptando este volumen finito ocupado en
es la constante de Planck4. Aceptando este volumen finito ocupado en 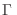 por cada estado, la integración de la expresión anterior abarca estados con energías levemente superiores a
por cada estado, la integración de la expresión anterior abarca estados con energías levemente superiores a 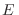 en una cantidad
en una cantidad
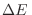 pequeña, aunque el volumen abarcado en el espacio de las fases es mucho mayor que el de un único estado.
pequeña, aunque el volumen abarcado en el espacio de las fases es mucho mayor que el de un único estado.
Al maximizar la entropía en esta descripción clásica se obtiene
donde
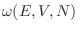 es el volumen en
es el volumen en 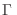 comprendido entre las
superficies de energía
comprendido entre las
superficies de energía 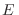 y
y
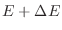
que también puede representarse como el área
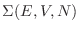 de la
hipersuperficie con energía
de la
hipersuperficie con energía 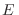 multiplicada por el ancho
multiplicada por el ancho 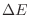 ,
,
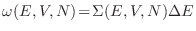 . La densidad de probabilidad se anula
si el estado analizado no se encuentra comprendido en
. La densidad de probabilidad se anula
si el estado analizado no se encuentra comprendido en
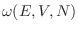 .
Reemplazando la expresión hallada para
.
Reemplazando la expresión hallada para
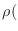
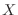
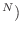 en la definición
de entropía, se obtiene
en la definición
de entropía, se obtiene
![$\displaystyle \fbox{ $\displaystyle S(E,V,N) = k \ln \frac{\omega(E,V,N)}{C^N}
\rule[-1.75em]{0em}{4.5em} $ }$](img409.png) |
(11) |
Esta expresión es equivalente a la desarrollada para el caso cuántico: si
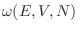 es el volumen en
es el volumen en 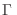 ocupado por todos los estados
accesibles y
ocupado por todos los estados
accesibles y 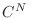 es el volumen asociado a un solo estado,
es el volumen asociado a un solo estado,
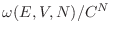 es el número de estados compatibles con la energía
es el número de estados compatibles con la energía
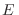 prefijada. Por otro lado, la expresión encontrada para
prefijada. Por otro lado, la expresión encontrada para 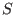 puede
tomarse como relación fundamental a partir de la cual pueden derivarse todas
las propiedades termodinámicas del sistema considerado.
puede
tomarse como relación fundamental a partir de la cual pueden derivarse todas
las propiedades termodinámicas del sistema considerado.
Es interesante verificar que esta expresión para la entropía resulta extensiva. Para ello consideremos un sistema con 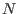 partículas
distinguibles dividido en dos partes no interactuantes, conteniendo cada
subsistema
partículas
distinguibles dividido en dos partes no interactuantes, conteniendo cada
subsistema 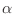 y
y
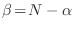 partículas respectivamente. El
hamiltoniano del sistema conjunto puede escribirse como
partículas respectivamente. El
hamiltoniano del sistema conjunto puede escribirse como
y el espacio de las fases es el producto cartesiano de los respectivos
espacios para cada subsistema,
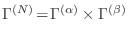 . Un estado con
energía total
. Un estado con
energía total 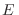 se logra combinando un estado del subsistema
se logra combinando un estado del subsistema 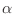 cuya energía parcial es
cuya energía parcial es 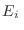 con un estado de
con un estado de 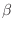 cuya energía es
cuya energía es
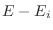 , lo que en el espacio
, lo que en el espacio
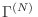 implica un volumen
implica un volumen
Como esta no es la única alternativa, ya que existen muchos valores de 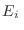 que se corresponden con la misma energía total
que se corresponden con la misma energía total 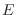 , el volumen en el espacio
, el volumen en el espacio
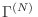 que debemos evaluar resulta de sumar todas las combinaciones posibles, es decir
que debemos evaluar resulta de sumar todas las combinaciones posibles, es decir
Si el mayor sumando en esta expresión se da cuando
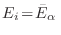 (
(
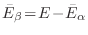 ), podemos acotar
), podemos acotar 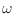 por arriba
reemplazando en la sumatoria todos los términos por ese valor máximo, y por
abajo eliminando todos los otros términos (que son no negativos):
por arriba
reemplazando en la sumatoria todos los términos por ese valor máximo, y por
abajo eliminando todos los otros términos (que son no negativos):
Tomando logaritmos y multiplicando por 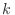 obtenemos
obtenemos
donde hemos identificado
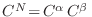 a partir de su
definición. Cualquier volumen en el espacio
a partir de su
definición. Cualquier volumen en el espacio 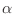 (o
(o 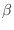 ) es
proporcional a cierta cantidad (dependiente del volumen en cuestión) elevada
a una potencia
) es
proporcional a cierta cantidad (dependiente del volumen en cuestión) elevada
a una potencia 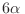 (o
(o 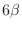 ), de manera que el primer término del
miembro de la derecha es proporcional a
), de manera que el primer término del
miembro de la derecha es proporcional a
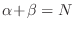 , mientras que el
segundo es proporcional a
, mientras que el
segundo es proporcional a 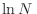 (pues
(pues
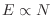 ). En el límite
termodinámico, es decir cuando
). En el límite
termodinámico, es decir cuando 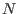 es muy grande (y también
es muy grande (y también 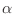 y
y
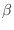 ), la contribución del último término es despreciable frente al
primero, coincidiendo entonces la cota inferior con la superior. Esto
implica que, en el límite termodinámico,
), la contribución del último término es despreciable frente al
primero, coincidiendo entonces la cota inferior con la superior. Esto
implica que, en el límite termodinámico,
de modo que la entropía es aditiva. La extensividad que deseábamos verificar
es consecuencia directa de la aditividad.
Con un razonamiento similar al anterior puede mostrarse que si
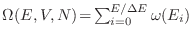 representa el volumen
contenido dentro de la hipersuperficie
representa el volumen
contenido dentro de la hipersuperficie
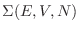 , la expresión para la
entropía puede escribirse también como
, la expresión para la
entropía puede escribirse también como
![$\displaystyle \fbox{ $\displaystyle S(E,V,N) = k \ln \frac{\Omega(E,V,N)}{C^N}
\rule[-1.75em]{0em}{4.5em} $ }$](img438.png) |
(12) |
Matemáticamente esta expresión suele resultar más sencilla en la práctica, de modo
que la utilizaremos en lugar de la fórmula (11) cuando sea conveniente.
Paralelamente a la demostración anterior, hemos resaltado el hecho de que la
energía
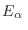 del subsistema
del subsistema 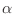 tiene en realidad un valor
bien definido, ya que --siempre en el límite termodinámico-- la sumatoria
puede reemplazarse por un único sumando: el término que maximiza
tiene en realidad un valor
bien definido, ya que --siempre en el límite termodinámico-- la sumatoria
puede reemplazarse por un único sumando: el término que maximiza
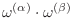 bajo la restricción
bajo la restricción
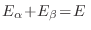 (cte). Como el logaritmo es una función monótonamente
creciente, la condición de máximo puede escribirse como
(cte). Como el logaritmo es una función monótonamente
creciente, la condición de máximo puede escribirse como
Dado que los subsistemas son independientes,
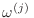 sólo depende
de
sólo depende
de 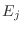 , de modo que la condición anterior implica
, de modo que la condición anterior implica
para
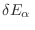 arbitrario, es decir
arbitrario, es decir
Esta identidad es un nuevo indicio de la “razonabilidad” de asociar la
entropía de información con la entropía termodinámica, pues si
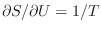 , la identidad anterior significa que
, la identidad anterior significa que
es decir, en el equilibrio las temperaturas de ambos subsistemas deben
igualarse. Por conveniencia, en la definición de la entropía se elige la constante
de Boltzmann
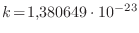 J/K 5, con el objeto de que esta temperatura coincida con la temperatura absoluta que se introduce en la termodinámica. De todos modos, en la expresión (9) se ha explicitado que la elección de esta
magnitud es de algún modo irrelevante, ya que está ligada a los valores de
los multiplicadores de Lagrange, y modificarla solo representaría un cambio
de unidades.
J/K 5, con el objeto de que esta temperatura coincida con la temperatura absoluta que se introduce en la termodinámica. De todos modos, en la expresión (9) se ha explicitado que la elección de esta
magnitud es de algún modo irrelevante, ya que está ligada a los valores de
los multiplicadores de Lagrange, y modificarla solo representaría un cambio
de unidades.
Finalmente, es fácil ver que nuestra expresión para la entropía crece con la
energía interna: al aumentar 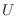 , el volumen
, el volumen 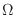 que debe evaluarse
en la expresión (12) crece, pues pasamos a abarcar, además de los
estados anteriores, nuevos estados con energía interna algo mayor. Como el
logaritmo es una función creciente, esto significa que
que debe evaluarse
en la expresión (12) crece, pues pasamos a abarcar, además de los
estados anteriores, nuevos estados con energía interna algo mayor. Como el
logaritmo es una función creciente, esto significa que 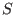 crece con
crece con 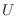 .
La expresión que aceptamos para la entropía estadística satisface entonces
los requisitos que exigimos al introducir esta función para desarrollar la
teoría termodinámica: por un lado, toma el máximo valor compatible con
.
La expresión que aceptamos para la entropía estadística satisface entonces
los requisitos que exigimos al introducir esta función para desarrollar la
teoría termodinámica: por un lado, toma el máximo valor compatible con 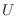 ,
,
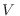 (o la variable extensiva
(o la variable extensiva 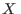 que corresponda) y
que corresponda) y 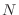 ; por otro, es
una función monótonamente creciente con
; por otro, es
una función monótonamente creciente con 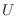 , y además cumple con la propiedad de aditividad.
, y además cumple con la propiedad de aditividad.
Subsecciones
Gustavo Castellano 19/11/2021
![]() es fija, dispone de muchos microestados compatibles
con la condición
es fija, dispone de muchos microestados compatibles
con la condición ![]() (constante). El ensamble asociado con esta
situación se denomina microcanónico.
(constante). El ensamble asociado con esta
situación se denomina microcanónico.
![]() con el único vínculo
con el único vínculo
![]() implica un procedimiento similar al de la sección anterior, aunque en este
caso representaremos como
implica un procedimiento similar al de la sección anterior, aunque en este
caso representaremos como
![]() a las variaciones que se
provoquen en el operador
a las variaciones que se
provoquen en el operador
![]() que maximiza la entropía:
que maximiza la entropía:
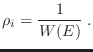
![]() en la expresión para la entropía
obtenemos nuevamente
en la expresión para la entropía
obtenemos nuevamente
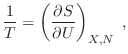
![]()
![]()
![]() , y la entropía se escribe
, y la entropía se escribe
![$\displaystyle S = - k \int_{E<H(\mbox{\scriptsize {\boldmath$X$}$^N$})<E+\Delta...
...mbox{\boldmath${X}$}^N) \ln\left[C^N\rho(\mbox{\boldmath${X}$}^N)\right] \;,
$](img395.png)
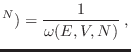
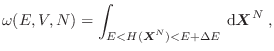
![]() es el volumen en
es el volumen en ![]() ocupado por todos los estados
accesibles y
ocupado por todos los estados
accesibles y ![]() es el volumen asociado a un solo estado,
es el volumen asociado a un solo estado,
![]() es el número de estados compatibles con la energía
es el número de estados compatibles con la energía
![]() prefijada. Por otro lado, la expresión encontrada para
prefijada. Por otro lado, la expresión encontrada para ![]() puede
tomarse como relación fundamental a partir de la cual pueden derivarse todas
las propiedades termodinámicas del sistema considerado.
puede
tomarse como relación fundamental a partir de la cual pueden derivarse todas
las propiedades termodinámicas del sistema considerado.
![]() partículas
distinguibles dividido en dos partes no interactuantes, conteniendo cada
subsistema
partículas
distinguibles dividido en dos partes no interactuantes, conteniendo cada
subsistema ![]() y
y
![]() partículas respectivamente. El
hamiltoniano del sistema conjunto puede escribirse como
partículas respectivamente. El
hamiltoniano del sistema conjunto puede escribirse como
![$\displaystyle \omega(E) = \sum_{i=1}^{E/\Delta E}
\left[ \omega^{(\alpha)}(E_i) \cdot \omega^{(\beta)}(E-E_i) \right] \;.
$](img423.png)
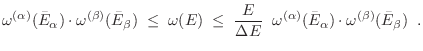
![$\displaystyle k \ln \left[ \frac{\omega^{(\alpha)}(\bar{E}_\alpha)}{C^\alpha}...
...^{(\beta)}(\bar{E}_\beta)}{C^\beta} \right] +
k \ln \frac E{\Delta E} \;\;,
$](img428.png)
![]() representa el volumen
contenido dentro de la hipersuperficie
representa el volumen
contenido dentro de la hipersuperficie
![]() , la expresión para la
entropía puede escribirse también como
, la expresión para la
entropía puede escribirse también como
![]() del subsistema
del subsistema ![]() tiene en realidad un valor
bien definido, ya que --siempre en el límite termodinámico-- la sumatoria
puede reemplazarse por un único sumando: el término que maximiza
tiene en realidad un valor
bien definido, ya que --siempre en el límite termodinámico-- la sumatoria
puede reemplazarse por un único sumando: el término que maximiza
![]() bajo la restricción
bajo la restricción
![]() (cte). Como el logaritmo es una función monótonamente
creciente, la condición de máximo puede escribirse como
(cte). Como el logaritmo es una función monótonamente
creciente, la condición de máximo puede escribirse como
![$\displaystyle \left[ \frac{\partial\ln\omega^{(\alpha)}}{\partial E_\alpha} -
\frac{\partial\ln\omega^{(\beta)}}{\partial E_\beta} \right]
\delta E_\alpha = 0
$](img445.png)
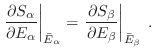
![]() , el volumen
, el volumen ![]() que debe evaluarse
en la expresión (12) crece, pues pasamos a abarcar, además de los
estados anteriores, nuevos estados con energía interna algo mayor. Como el
logaritmo es una función creciente, esto significa que
que debe evaluarse
en la expresión (12) crece, pues pasamos a abarcar, además de los
estados anteriores, nuevos estados con energía interna algo mayor. Como el
logaritmo es una función creciente, esto significa que ![]() crece con
crece con ![]() .
La expresión que aceptamos para la entropía estadística satisface entonces
los requisitos que exigimos al introducir esta función para desarrollar la
teoría termodinámica: por un lado, toma el máximo valor compatible con
.
La expresión que aceptamos para la entropía estadística satisface entonces
los requisitos que exigimos al introducir esta función para desarrollar la
teoría termodinámica: por un lado, toma el máximo valor compatible con ![]() ,
,
![]() (o la variable extensiva
(o la variable extensiva ![]() que corresponda) y
que corresponda) y ![]() ; por otro, es
una función monótonamente creciente con
; por otro, es
una función monótonamente creciente con ![]() , y además cumple con la propiedad de aditividad.
, y además cumple con la propiedad de aditividad.