El problema central en el caso cuántico también es contar los estados de
nuestro sistema compatibles con el valor de energía 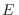 preestablecido.
preestablecido.
Veremos en primer lugar el caso de 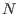 espines
espines 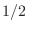 no interactuantes en
un sólido bajo la acción de un campo externo
no interactuantes en
un sólido bajo la acción de un campo externo 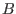 . Las energías posibles
para cada espín son
. Las energías posibles
para cada espín son
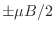 , de modo que las energías totales para todo
el sistema serán
, de modo que las energías totales para todo
el sistema serán
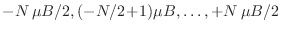 . Denotando el
valor de la energía como
. Denotando el
valor de la energía como
debemos entonces evaluar el número de formas 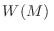 en que pueden
combinarse
en que pueden
combinarse 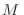 espines alineados con el campo con
espines alineados con el campo con 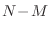 desalineados. Se
deja como ejercicio resolver este problema combinatorio, válido para
cualquier sistema en el que sus componentes pueden acceder solo a 2 estados
cuyas energías suelen denotarse como 0 y
desalineados. Se
deja como ejercicio resolver este problema combinatorio, válido para
cualquier sistema en el que sus componentes pueden acceder solo a 2 estados
cuyas energías suelen denotarse como 0 y 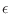 . Este problema es
conocido como sistema de dos niveles (por razones desconocidas), y
puede verse que para temperaturas extremas se anulan los valores asintóticos
para el calor específico por distintos motivos. En el límite de bajas
temperaturas, la misma definición de calor específico
. Este problema es
conocido como sistema de dos niveles (por razones desconocidas), y
puede verse que para temperaturas extremas se anulan los valores asintóticos
para el calor específico por distintos motivos. En el límite de bajas
temperaturas, la misma definición de calor específico
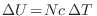 nos hace ver que la cuántica prohíbe a nuestro sistema
absorber cantidades infinitesimales de energía (calor) puesto que existe un
umbral discreto entre el nivel fundamental y el primer nivel excitado para
nuestro sistema6. Para temperaturas altas, como los niveles de energía son acotados,
una vez que el sistema absorbió el máximo de energía posible, no importa
si el baño térmico que lo circunda aumenta su temperatura, pues ya no puede
seguir incrementando su energía
nos hace ver que la cuántica prohíbe a nuestro sistema
absorber cantidades infinitesimales de energía (calor) puesto que existe un
umbral discreto entre el nivel fundamental y el primer nivel excitado para
nuestro sistema6. Para temperaturas altas, como los niveles de energía son acotados,
una vez que el sistema absorbió el máximo de energía posible, no importa
si el baño térmico que lo circunda aumenta su temperatura, pues ya no puede
seguir incrementando su energía 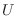 .
.
El segundo ejemplo que abordaremos aquí consiste en el modelo de Einstein
para el sólido cristalino. La descripción termodinámica que se busca para el
sistema sólo tiene en cuenta las oscilaciones colectivas del sólido
(ignorando la contribución de los electrones, efectos de superficie, etc.).
Esto significa considerar únicamente las interacciones armónicas entre los 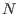 núcleos del sólido descripto, que se representan mediante un sistema de
núcleos del sólido descripto, que se representan mediante un sistema de
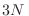 osciladores acoplados. Sabemos que esto significa que habrá
osciladores acoplados. Sabemos que esto significa que habrá 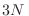 modos normales (osciladores desacoplados), y la simplificación de este modelo es que
todos los osciladores poseen la misma frecuencia
modos normales (osciladores desacoplados), y la simplificación de este modelo es que
todos los osciladores poseen la misma frecuencia 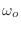 7.
7.
El 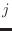 -ésimo oscilador puede tomar valores de energía
-ésimo oscilador puede tomar valores de energía
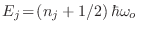 con
con
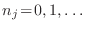 La energía total del sistema será entonces
La energía total del sistema será entonces
La pregunta entonces, dentro del esquema microcanónico es ¿de cuántas
maneras 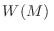 se puede lograr el valor de energía
se puede lograr el valor de energía 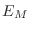 ? En otras
palabras, ¿de cuántas maneras pueden sumarse
? En otras
palabras, ¿de cuántas maneras pueden sumarse 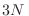 números enteros mayores
o iguales que 0 para obtener el valor
números enteros mayores
o iguales que 0 para obtener el valor 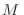 (fijo)? Otra vez la respuesta se
logra mediante un análisis combinatorio que se deja como ejercicio. También
en este caso se verifica que el calor específico se anula para
(fijo)? Otra vez la respuesta se
logra mediante un análisis combinatorio que se deja como ejercicio. También
en este caso se verifica que el calor específico se anula para 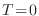 , tal
como lo predice la cuántica. Para el límite de altas temperaturas puede verse
que el calor específico se vuelve constante, tal como debemos esperar de
acuerdo con el teorema de equipartición de la energía que veremos en el
próximo capítulo.
, tal
como lo predice la cuántica. Para el límite de altas temperaturas puede verse
que el calor específico se vuelve constante, tal como debemos esperar de
acuerdo con el teorema de equipartición de la energía que veremos en el
próximo capítulo.
Gustavo Castellano 19/11/2021
![]() preestablecido.
preestablecido.
![]() espines
espines ![]() no interactuantes en
un sólido bajo la acción de un campo externo
no interactuantes en
un sólido bajo la acción de un campo externo ![]() . Las energías posibles
para cada espín son
. Las energías posibles
para cada espín son
![]() , de modo que las energías totales para todo
el sistema serán
, de modo que las energías totales para todo
el sistema serán
![]() . Denotando el
valor de la energía como
. Denotando el
valor de la energía como
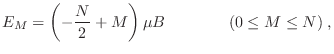
![]() núcleos del sólido descripto, que se representan mediante un sistema de
núcleos del sólido descripto, que se representan mediante un sistema de
![]() osciladores acoplados. Sabemos que esto significa que habrá
osciladores acoplados. Sabemos que esto significa que habrá ![]() modos normales (osciladores desacoplados), y la simplificación de este modelo es que
todos los osciladores poseen la misma frecuencia
modos normales (osciladores desacoplados), y la simplificación de este modelo es que
todos los osciladores poseen la misma frecuencia ![]() 7.
7.
![]() -ésimo oscilador puede tomar valores de energía
-ésimo oscilador puede tomar valores de energía
![]() con
con
![]() La energía total del sistema será entonces
La energía total del sistema será entonces
