Paradoja de Gibbs
Podemos escribir la entropía en notación más compacta como
donde
Esta expresión es muy similar a la que habíamos obtenido al desarrollar la teoría termodinámica. Analicemos el caso en que un recipiente contiene dos gases diferentes a temperatura 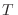 separados por una pared diatérmica, de modo que en un compartimiento hay
separados por una pared diatérmica, de modo que en un compartimiento hay 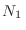 moléculas en un volumen
moléculas en un volumen 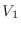 , mientras que en el otro hay
, mientras que en el otro hay 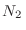 moléculas en un volumen
moléculas en un volumen 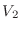 (
(
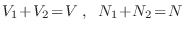 ). Al remover la pared divisoria, como
). Al remover la pared divisoria, como 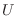 no cambia,
no cambia, 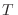 tampoco varía, de modo que al mezclar habrá un aumento de entropía dado por
tampoco varía, de modo que al mezclar habrá un aumento de entropía dado por
Cuando los gases son diferentes, esta expresión aparentemente provee una adecuada predicción. Sin embargo, si los gases son idénticos, aun cuando el sistema sea homogéneo antes de remover la pared divisoria (
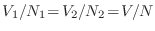 ), esta expresión señala que habrá un aumento en la entropía del sistema. Por supuesto, este resultado es absurdo, y para resolver este problema Gibbs introdujo una modificación en la constante
), esta expresión señala que habrá un aumento en la entropía del sistema. Por supuesto, este resultado es absurdo, y para resolver este problema Gibbs introdujo una modificación en la constante 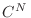 para el caso de partículas indistinguibles, agregándole un factor
para el caso de partículas indistinguibles, agregándole un factor 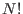 , es decir
, es decir
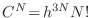 De este modo, utilizando la aproximación de Stirling la expresión para la entropía resulta
De este modo, utilizando la aproximación de Stirling la expresión para la entropía resulta
Esta expresión se conoce como ecuación de Sackur-Tetrode, y ahora es completamente coincidente con la que habíamos obtenido en Termo I (en particular, a diferencia de la expresión anterior, esta entropía sí es extensiva). La predicción del aumento de entropía se mantiene, excepto para el caso en que el sistema conjunto esté originalmente en equilibrio termodinámico, con igual temperatura y presión a ambos lados de la pared divisoria.
No hay una respuesta convincente acerca de por qué corresponde dividir
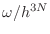 u
u
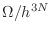 por
por 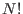 dentro del formalismo clásico.
Quizás la motivación original surgió de pensar que si las partículas son
indistinguibles, existen
dentro del formalismo clásico.
Quizás la motivación original surgió de pensar que si las partículas son
indistinguibles, existen 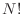 permutaciones que proveen el mismo estado,
aunque está claro que dentro de la teoría clásica todas las partículas son
distinguibles. La verdadera respuesta es en realidad provista por la
cuántica, en el marco de la llamada “segunda cuantización”: como veremos
más adelante, para describir
permutaciones que proveen el mismo estado,
aunque está claro que dentro de la teoría clásica todas las partículas son
distinguibles. La verdadera respuesta es en realidad provista por la
cuántica, en el marco de la llamada “segunda cuantización”: como veremos
más adelante, para describir 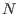 partículas idénticas, las funciones de
onda conjuntas deben ser simétricas o antisimétricas ante
permutaciones de partículas, y cuando las condiciones indican que la
descripción debe coincidir con el enfoque clásico, se ve que entonces ambas
formulaciones concuerdan gracias a ese denominador
partículas idénticas, las funciones de
onda conjuntas deben ser simétricas o antisimétricas ante
permutaciones de partículas, y cuando las condiciones indican que la
descripción debe coincidir con el enfoque clásico, se ve que entonces ambas
formulaciones concuerdan gracias a ese denominador 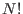 .
.
Gustavo Castellano 19/11/2021
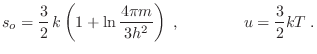
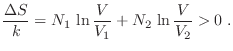
![$\displaystyle \fbox{ $\displaystyle S = \frac32 Nk\left(\frac53 +
\ln\f...
...t) + Nk \ln\left(\frac VN u^{3/2}\right)
\rule[-1.75em]{0em}{4em} $ }
$](img490.png)
![]() u
u
![]() por
por ![]() dentro del formalismo clásico.
Quizás la motivación original surgió de pensar que si las partículas son
indistinguibles, existen
dentro del formalismo clásico.
Quizás la motivación original surgió de pensar que si las partículas son
indistinguibles, existen ![]() permutaciones que proveen el mismo estado,
aunque está claro que dentro de la teoría clásica todas las partículas son
distinguibles. La verdadera respuesta es en realidad provista por la
cuántica, en el marco de la llamada “segunda cuantización”: como veremos
más adelante, para describir
permutaciones que proveen el mismo estado,
aunque está claro que dentro de la teoría clásica todas las partículas son
distinguibles. La verdadera respuesta es en realidad provista por la
cuántica, en el marco de la llamada “segunda cuantización”: como veremos
más adelante, para describir ![]() partículas idénticas, las funciones de
onda conjuntas deben ser simétricas o antisimétricas ante
permutaciones de partículas, y cuando las condiciones indican que la
descripción debe coincidir con el enfoque clásico, se ve que entonces ambas
formulaciones concuerdan gracias a ese denominador
partículas idénticas, las funciones de
onda conjuntas deben ser simétricas o antisimétricas ante
permutaciones de partículas, y cuando las condiciones indican que la
descripción debe coincidir con el enfoque clásico, se ve que entonces ambas
formulaciones concuerdan gracias a ese denominador ![]() .
.