Diamagnetismo de Landau (basado en el texto de Huang)

Ya hemos visto en uno de los ejercicios el teorema de Van Leewen, que establece que no existe el diamagnetismo (y el magnetismo en general) en estadística clásica. Sin embargo Landau en 1930 mostró que es posible explicar el fenómeno del diamagnetismo mediante la cuantización de las órbitas de partículas cargadas en un campo magnético.

Las propiedades magnéticas de un material se analizan a través de la susceptibilidad magnética por unidad de volumen

$$\chi = \left(\frac{\partial M'}{\partial B}\right)_T \;.$$

Aquí $M'$ representa el momento magnético por unidad de volumen, y $B$, la inducción externa aplicada. Si el análisis es llevado adelante en el ensamble canónico, sabemos que cuando el hamiltoniano incorpora el acoplamiento con el campo externo, la función partición estará relacionada con la energía libre de Gibbs

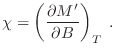
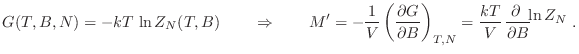
$$G(T,B,N) = -kT \ln Z_N(T,B) \qquad \Rightarrow \qquad M' = -\fr... ...,N} = \frac{kT}V \frac{\partial }{\partial B}\!{}^{\displaystyle\ln Z_N} \;.$$

En el gran canónico el análisis es similar, resultando

$$M' = - \left[\frac{\partial }{\partial B} \left(\frac{\widetilde... ...ac{\partial }{\partial B} \left(\frac{\ln Z_\mu}V\right)\right]_{T(,V),z} \;.$$

Hemos denotado el gran potencial como $\widetilde\Omega$ para recordar que a diferencia de los casos anteriores, éste involucra también la transformación de Legendre de $M$ por $B$ (otra vez, en virtud de que el hamiltoniano utilizado para el cálculo de la gran partición incluye el acoplamiento con la fuente de campo). Por otro lado, aunque en general las variables $P$ y $V$ no intervienen en las ecuaciones de estado, se ha indicado a $V$ como otra posible variable natural de nuestro potencial.

Un sistema es diamagnético cuando $\chi<0$, y paramagnético cuando $\chi>0$. Los núcleos que constituyen una red cristalina en general no aportan a la respuesta magnética de los materiales, pues su momento magnético intrínseco es mucho menor que el de los electrones (típicamente 1000 veces más chico). El alineamiento del espín de los electrones con el campo externo da lugar al paramagnetismo, que compite con el movimiento orbital de los mismos. Para llevar adelante nuestro análisis, pensamos en un gas de electrones libres, ignorando entonces sus coordenadas de espín al estudiar su traslación.