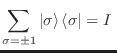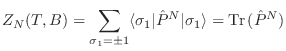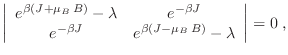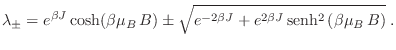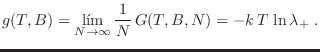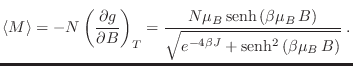La descripción de un sistema unidimensional se simplifica notablemente
cuando se imponen condiciones de contorno periódicas, es decir, el estado
del núcleo 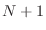 coincide con el del núcleo 1. Entonces podemos escribir
coincide con el del núcleo 1. Entonces podemos escribir
Para calcular la función partición, solo debe tenerse la precaución de
barrer todos los autovalores de este hamiltoniano, a través de la acción de
los operadores
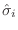 , que actúan cada uno en el espacio de
Hilbert correspondiente, con autovalores
, que actúan cada uno en el espacio de
Hilbert correspondiente, con autovalores
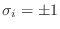
Definimos ahora el operador 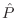 con elementos de matriz
con elementos de matriz
Eligiendo la base de manera que el autovalor
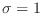 corresponda al
elemento
corresponda al
elemento
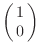 y
y
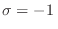 al
al
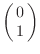 , la
representación matricial de este operador es
, la
representación matricial de este operador es
De este modo, la función partición resulta
Como los estados
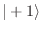 y
y
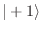 forman una base,
forman una base,
de manera que
Al ser 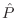 un operador simétrico, puede diagonalizarse exigiendo
un operador simétrico, puede diagonalizarse exigiendo
resultando la ecuación característica
de donde
Como
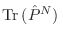 no depende de la base
no depende de la base
Es fácil ver que en el límite termodinámico solo sobrevive la contribución
de
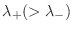 analizando la energía libre de Gibbs por
núcleo
analizando la energía libre de Gibbs por
núcleo
El momento magnético total para el sistema resulta
Es evidente entonces que cuando 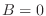 ,
,
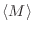 también se
anula, es decir, no hay magnetización espontánea en una dimensión.
también se
anula, es decir, no hay magnetización espontánea en una dimensión.
Gustavo Castellano 19/11/2021
![]() coincide con el del núcleo 1. Entonces podemos escribir
coincide con el del núcleo 1. Entonces podemos escribir
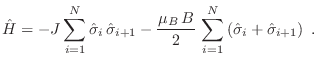
![$\displaystyle Z_N(T,B) = \sum_{\sigma_1=\pm1}\cdots\sum_{\sigma_N=\pm1}
e^{\be...
...gma_{i+1} +
{\textstyle\frac{\mu_B\,B}2}\,(\sigma_i+\sigma_{i+1})\right]} \;.
$](img1144.png)
![$\displaystyle \langle\sigma_i\vert\hat P\vert\sigma_{i+1}\rangle =
e^{\beta\le...
...gma_{i+1} +
{\textstyle\frac{\mu_B\,B}2}\,(\sigma_i+\sigma_{i+1})\right]} \;.
$](img1146.png)
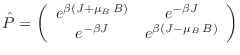
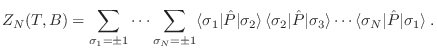
![]() y
y
![]() forman una base,
forman una base,