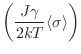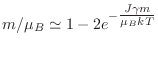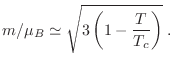En dos dimensiones, el modelo de Ising también puede resolverse
analíticamente, lográndose encontrar respuesta ferromagnética bajo campos
externos. Sin embargo, el desarrollo se torna excesivamente complicado para
sistemas tridimensionales, recurriéndose a métodos aproximados. El que
veremos aquí se conoce como método de Weiss o modelo de campo
molecular.
En esta descripción se reemplaza la interacción con los 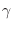 primeros
vecinos de la red por un promedio, de modo que el hamiltoniano resulta
primeros
vecinos de la red por un promedio, de modo que el hamiltoniano resulta
El denominador 2 del primer miembro se introduce para evitar contar dos
veces la interacción correspondiente a cada par
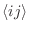 . Vemos
entonces que el efecto de los primeros vecinos se traduce como la producción
de un campo efectivo
. Vemos
entonces que el efecto de los primeros vecinos se traduce como la producción
de un campo efectivo
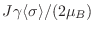 . En esta
aproximación de campo medio puede entonces escribirse
. En esta
aproximación de campo medio puede entonces escribirse
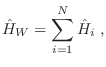 con
con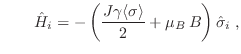
es decir, como un sistema de espines no interactuantes. Al ser
independientes los espines, sabemos que la función partición del sistema
total 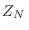 se evalúa a partir de la partición correspondiente a cada
espín
se evalúa a partir de la partición correspondiente a cada
espín 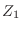 , pues
, pues 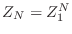 . En nuestro caso conocemos el resultado
. En nuestro caso conocemos el resultado
y, a partir de los autovalores 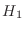 del hamiltoniano para cada espín,
del hamiltoniano para cada espín,
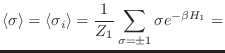 tgh
tgh![$\displaystyle \left[ \beta \left( \frac{J\gamma\langle\sigma\rangle}2 +
\mu_B\,B \right)\right] \;.
$](img1177.png)
Esta ecuación trascendente puede tener solución no nula para 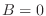 , como
puede verificarse gráficamente. También se deja como ejercicio comprobar que
existe una temperatura crítica por encima de la cual las soluciones
no triviales no existen, cuyo valor es
, como
puede verificarse gráficamente. También se deja como ejercicio comprobar que
existe una temperatura crítica por encima de la cual las soluciones
no triviales no existen, cuyo valor es
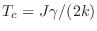 .
.
Por supuesto como esta descripción del fenómeno del ferromagnetismo no
depende de la dimensión de nuestro problema, resulta inadecuada para un
sistema unidimensional.
De la “ecuación de Curie-Weiss” correspondiente a 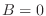
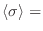 tgh
tgh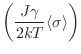
podemos hallar (numéricamente) el comportamiento del momento magnético
por núcleo
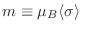 en función de la
temperatura. Pueden encontrarse las aproximaciones asintóticas para
en función de la
temperatura. Pueden encontrarse las aproximaciones asintóticas para 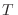 bajas
bajas
y para
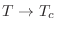 (por debajo)
(por debajo)
De este modo pueden analizarse todos los exponentes críticos,
relacionados con los comportamientos de los diferentes parámetros cerca del
punto crítico.
Gustavo Castellano 19/11/2021
![]() primeros
vecinos de la red por un promedio, de modo que el hamiltoniano resulta
primeros
vecinos de la red por un promedio, de modo que el hamiltoniano resulta
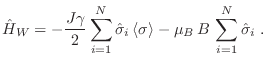
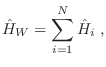 con
con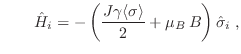
![$\displaystyle Z_1 = 2 \cosh \left[ \beta \left( \frac{J\gamma\langle\sigma\rangle}2 +
\mu_B\,B \right)\right]
$](img1174.png)
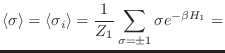 tgh
tgh![$\displaystyle \left[ \beta \left( \frac{J\gamma\langle\sigma\rangle}2 +
\mu_B\,B \right)\right] \;.
$](img1177.png)
![]()