Subir: Gas de Fermi-Dirac Anterior: El potencial de Gibbs
Una aplicación interesante del modelo de Ising es el de un gas imaginado
como un conjunto de ![]() sitios de red (de Bravais) fijos, en los
cuales pueden acomodarse las moléculas que conforman el gas. La energía
cinética de las moléculas no es tenida en cuenta, y se considera que el
potencial de interacción entre las partículas depende sólo de la distancia
entre ellas
sitios de red (de Bravais) fijos, en los
cuales pueden acomodarse las moléculas que conforman el gas. La energía
cinética de las moléculas no es tenida en cuenta, y se considera que el
potencial de interacción entre las partículas depende sólo de la distancia
entre ellas
![]() . Si tomamos el parámetro de red
como la unidad, el potencial puede expresarse como
. Si tomamos el parámetro de red
como la unidad, el potencial puede expresarse como
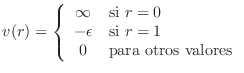
A cada sitio ![]() entonces podemos asociar un número de ocupación
entonces podemos asociar un número de ocupación ![]() ó 1 (vacío o con una sola partícula). Para una determinada configuración
ó 1 (vacío o con una sola partícula). Para una determinada configuración
![]() los autovalores del hamiltoniano correspondiente a
este sistema estarán dados por
los autovalores del hamiltoniano correspondiente a
este sistema estarán dados por
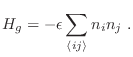
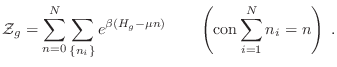
Mediante la sustitución
![]() , con
, con
![]() ,
podemos reescribir
,
podemos reescribir
![$\displaystyle H_g = -\frac{\epsilon}4 \left[ \sum_{\langle ij\rangle}
\left(\s...
...m_{\langle ij\rangle} \sigma_i\sigma_j \right] -
\frac{\gamma N\epsilon}8 \;.
$](img1221.png)
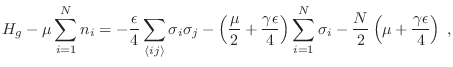
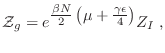
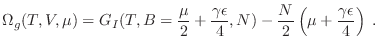
En este gas de red la densidad de partículas por unidad de volumen
![]() debe asociarse con la cantidad
debe asociarse con la cantidad
![]() . Aunque el modelo es muy simple,
se predicen adecuadamente isotermas similares a las del gas de Van der
Waals, recurriendo a la identidad
. Aunque el modelo es muy simple,
se predicen adecuadamente isotermas similares a las del gas de Van der
Waals, recurriendo a la identidad
![]() .
.
Gustavo Castellano 24/11/2020