A partir de la función partición es posible escribir una expresión para la
energía libre de Gibbs para (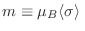 )
)
en particular para 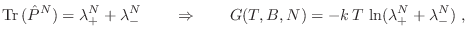 . En ese caso, para
. En ese caso, para 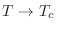 ,
,
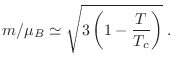 (pues
(pues
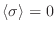 ). La expresión anterior presenta la particularidad
de que representa una función de
). La expresión anterior presenta la particularidad
de que representa una función de 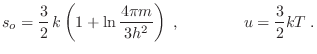 convexa, y por lo tanto no satisface
los criterios de estabilidad termodinámica (local). Para corregir este
inconveniente, tomamos un hamiltoniano de prueba
convexa, y por lo tanto no satisface
los criterios de estabilidad termodinámica (local). Para corregir este
inconveniente, tomamos un hamiltoniano de prueba
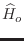 . Denotando
. Denotando
la función partición del sistema real (descripto por el hamiltoniano
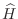 ) puede evaluarse como
) puede evaluarse como
donde
Como
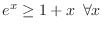 , para cualquier variable aleatoria
, para cualquier variable aleatoria 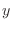 se
cumple
se
cumple
de manera que
es decir
Como esto debe valer para cualquier 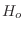 de prueba, elegimos el
correspondiente a espines no interactuantes
de prueba, elegimos el
correspondiente a espines no interactuantes
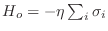 . De
este modo
. De
este modo
Buscamos entonces minimizar 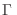 para cada valor de
para cada valor de 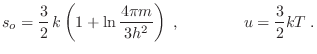 con
con
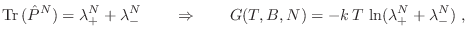 . Sabemos de antemano que
. Sabemos de antemano que
![$\displaystyle G_o = -kTN \ln \left[ 2 \cosh(\beta\eta) \right] \qquad {\rm y} \qquad
\langle\sigma_i\rangle_o = m_o/\mu_B =$](img1199.png) tgh
tgh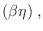
con lo cual
mientras que
En el último paso usamos el hecho de que se trata de espines no
interactuantes. Entonces tenemos
de manera que
El mínimo de esta expresión se dará cuando
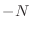 tgh
tgh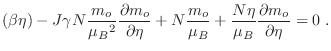
El primer término se cancela con el tercero, de modo el valor
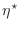 que minimiza
que minimiza 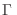 es
es
 , con lo cual
, con lo cual
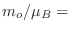 tgh
tgh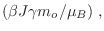
es decir, reobtenemos así la ecuación de Curie-Weiss (excepto por un
factor 2).
De esta manera, nuestra mejor estimación para 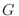 es
es
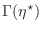
Afortunadamente, esta función es “termodinámicamente” cóncava, como puede
verificarse directamente.
Gustavo Castellano 24/11/2020
![]() )
)
![$\displaystyle G(T,B,N) = - kTN \ln \left\{ 2 \cosh\left[\beta \left(
\frac{J\gamma\langle\sigma\rangle}2 + \mu_B\,B \right) \right] \right\} \;,
$](img1182.png)
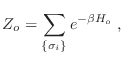
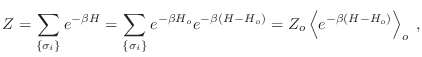
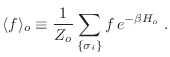
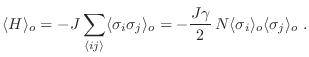
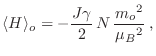
![$\displaystyle \Gamma(\eta) = -\frac{N}{\beta} \ln \left[2\cosh(\beta\eta)\right] -
\frac{J\gamma N}2\,\frac{m_oČ}{\mu_BČ} + N\eta\,\frac{m_o}{\mu_B} \;.
$](img1204.png)
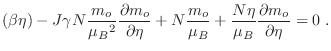
![]() es
es
![]()
![$\displaystyle G(T,B=0,N) =
- NkT \ln \left[2\cosh\left(\frac{Ti_c}{T}\,\frac{m_o}{\mu_B}\right)\right]
+ N\frac{kT_c}2\,\left(\frac{m_o}{\mu_B}\right)^2 \;.
$](img1213.png)