Introducción¶
Modelos atómicos¶
Como se deriva directamente de su nombre, la física atómica y la física nuclear nacen del estudio de los átomos y sus propiedades. A grandes rasgos, se puede decir que la primera tiene poco más de 200 años y la segunda recién ha cumplido su primer centenario, pero ambas datan de una idea que proviene de pensadores del siglo de oro de Pericles en la antigua Grecia. Demócrito y Leucipo, 400 años antes de Cristo, proponen una unidad de materia indivisible, eterna, homogénea, incompresible e invisible, en movimiento constante en el vacío y que entre sí solo se diferenciaba en tamaño, forma y posición: el átomo.
Tiempo después, Aristóteles sostuvo que todas las cosas estaban compuestas por cuatro elementos principales: agua, aire, fuego y tierra. También negó la existencia del vacío, por lo que daba lugar a la teoría del éter que llegó hasta el s. XX. Demócrito y su maestro Leucipo fueron fuertemente criticados al proponer una visión del mundo donde la materia estaba constituida por partículas indivisibles (\(\alpha\) -sin- y \(\tau \omicron \mu \omicron \nu\) -corte-) y que lo que no poseía átomos era simplemente vacío. Fueron así fundadores de una corriente conocida como atomismo. Aristóteles le dedicó mucho estudio y crítica a la obra de Demócrito, pero se dice que Platón directamente la despreciaba.
Las personas solemos asociar la historia del pensamiento a una sucesión ordenada de grandes genios o genias y hechos discretamente separados, sin tener en cuenta el verdadero proceso, algo que ningún ser racional puede aceptar como «forma ideal» pero que nos sirve para ordenar nuestro análisis cronológico acerca de una idea. Así, de Demócrito y su idea del átomo, saltamos directamente y sin escalas a Dalton, 2600 años después, y su «modelo atómico». Dalton, en 1807, propone al átomo como una unidad maciza y, sin mediar debates entre químicos y físicos, físicos y físicos, químicos y químicos, y todos estos con filósofos, nos volvemos a saltar casi 100 años y llegamos al modelo de Thomson en 1904.
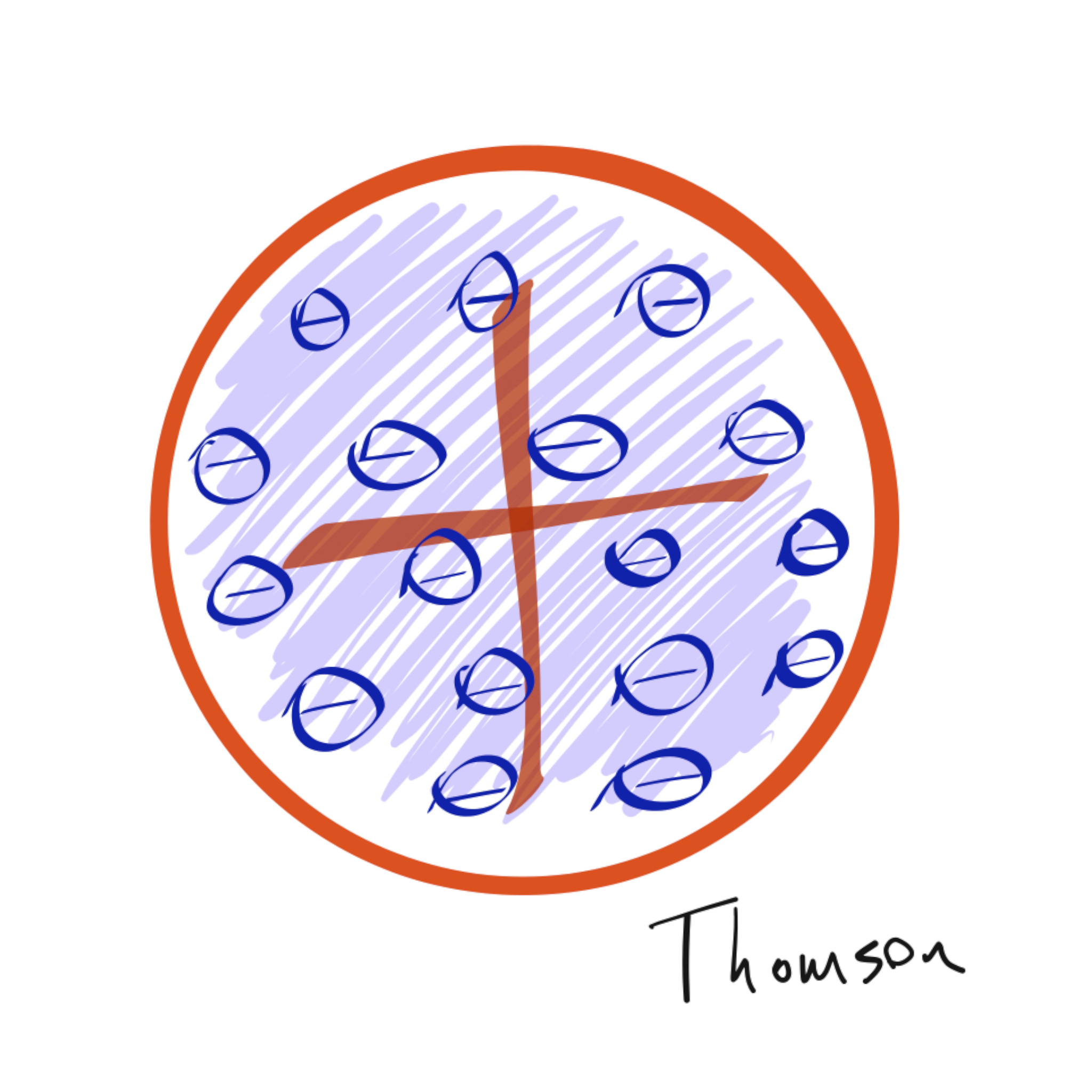
Ya con conocimientos de electricidad y habiendo descubierto el electrón, Thomson mantiene la idea de un átomo macizo pero sugiere que está compuesto además por electrones incrustados y homogéneamente distribuidos en una esfera homogénea de carga positiva, por su forma se lo conoce como «modelo de las pasas de pudín». Rutherford, en cambio, en 1911 propone que toda la carga positiva se encuentra concentrada en un núcleo donde además se concentra la mayor parte de la masa del átomo y los electrones se encuentran orbitando en el vacío, alrededor, lo que se conoce como el modelo planetario. Tan fuerte es el cambio propuesto por Rutherford y tal su impacto que es su modelo el que aún hoy asocia la mayoría de las personas con la idea de «átomo».
El modelo propuesto por Rutherford no puede explicar cuestiones básicas de las ecuaciones de Maxwell y «debería» emitir radiación hasta caer en el centro/núcleo, por lo que 2 años después Bohr en1913 propone un modelo en el cuál los electrones describen órbitas circulares sin irradiar energía, define que hay únicas órbitas permitidas fijadas por una expresión en función de un número entero \(n\) (el primer número atómico!) y que el electrón solo emite o absorbe energía cuando salta de una órbita a otra, siendo esta energía la diferencia entre los distintos niveles energéticos asociados a las órbitas posibles, dando lugar a los espectros de emisión.
Solo 3 años después, en 1916 Sommerfeld incorpora el segundo número atómico proponiendo subniveles de energía, además de órbitas elípticas. Pero una década después, basado en ideas de Planck y De Broglie, Schrödinger (1926) propone el modelo cuántico undulatorio no relativista donde los electrones son funciones de onda en nubes de probabilidad que decaen rápidamente al sobrepasar el radio atómico. Finalmente llegamos al modelo actual donde ya se habla de «orbitales» donde se maximiza la probabilidad de encontrar un electrón.
Modelo del átomo de Rutherford¶
Ernest Rutherford vivió 66 años entre agosto de 1871 y octubre de 1937 y, además de desempeñarse como académico, tuvo una destacada vida como político y gestor, llegando a ser miembro de la Cámara de los Lores y Presidente de la Real Sociedad. Alumno de Thomson, Nobel de Física (1906) que descubrió el electrón y famoso por el modelo de átomo que lleva su nombre, Rutherford también se hace con el premio Nobel pero en su caso, «lamentablemente» (consideraba a la física como la única y verdadera ciencia, «el resto es filatelía» afirmaba), el de Química en 1908. La grandeza del legado de este físico y químico inglés se puede inducir al saber que su tumba se encuentra en la Abadía de Westminster, junto a la de su propio maestro Thomson y las de los grandes genios Maxwell y Newton. Pero quizás, más impresión causa leer la lista de sus alumnos doctorales que alcanzaron también la máxima distinción en ciencias.
Tuvo más de 20 estudiantes de doctorado que revolucionaron la física y la química a nivel global. Entre los más conocidos se encuentran el alemán Hans Geiger (quien junto a Müller desarrolló el conocido contador que lleva su nombre), el premio Nobel de Física de 1922 Niels Bohr reconocido por sus contribuciones en el conocimiento de los átomos y la mecánica cuántica, el premio Nobel de 1950 Cecil Powell que descubrió el pión, el ruso Pyotr Leonidovich Kapitsa descubridor de la superfluidez, y los también Nobel Patrick Blackett, John Cockcroft, Ernest Walton, James Chadwick, Frederick Soddy y Edward Victor Appleton.
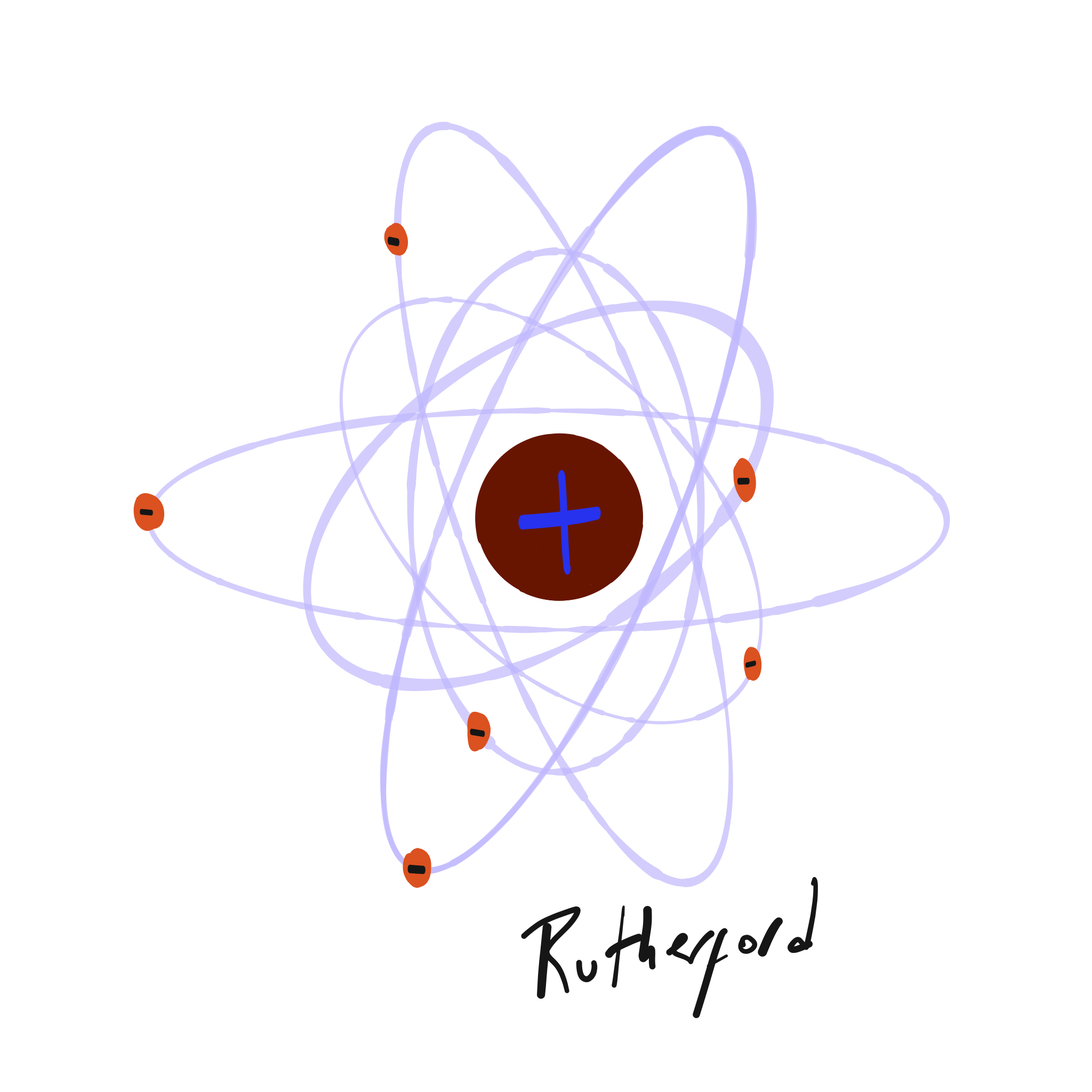
Rutherford es quien clasifica a las partículas radiactivas como alfa, beta y gamma y descubre que la radiactividad se encuentra acompañada de desintegraciones en los elementos. A diferencia de su maestro, quien había propuesto un modelo de átomo compuesto por electrones uniformemente distribuidos en un gas de carga positiva, Ernest propone en 1911 la carga positiva unificada en un núcleo compuesto por protones, en su centro, y electrones orbitando alrededor como si se tratase de planetas alrededor del sol. En el núcleo, propuso, no solo se reúne toda la carga positiva del átomo sino también la mayoría de su masa y, además, son los electrones los que definen el tamaño del átomo.
Figura 1: Modelos de átomo de Thomson (izq.) y de Rutherford (der.).
Así, la comprensión de la estructura atómica, pasó del modelo de pudín de pasas al modelo planetario de Rutherford que reflotó la idea que, años antes en 1904, había propuesto el físico japonés Hantarō Nagaoka.
Modelo de átomo de Bohr¶
Para explicar la estabilidad de los electrones, Bohr propone un modelo atómico en el cual se desplazan en órbitas circulares, mateniendo la idea de sistema planetario de Rutherford pero dividiendo los electrones en internos y externos (o «de valencia»), los cuales se encuentran en niveles definidos de energía a distancias energéticas fijas. Los niveles de energía se clasifican de forma creciente de acuerdo con la distancia al núcleo, así la órbita más cercana poseerá la menor energía permitida. Además, para cada órbita se definen un número máximo de electrones, permitiendo que en la primera órbita (llamada K) se ubiquen hasta 2 electrones, en la segunda (L) 8, en la tercera (M) 18, en las cuarta y quinta (N y O) 32, en la sexta (P) 18 y en la séptima (Q) 8. En los átomos, propuso, los electrones ocupan primero los niveles energéticos más bajos (capas internas) y después continúan los de energías superiores, generando la conocida «configuración electrónica». Así, por ejemplo, el Na que posee 11 \(e^-\) en total, tiene 2 en la primera capa, 8 en la segunda y 1 en la tercera (razón por la cual se ubica primero en la tercera fila de la tabla periódica).
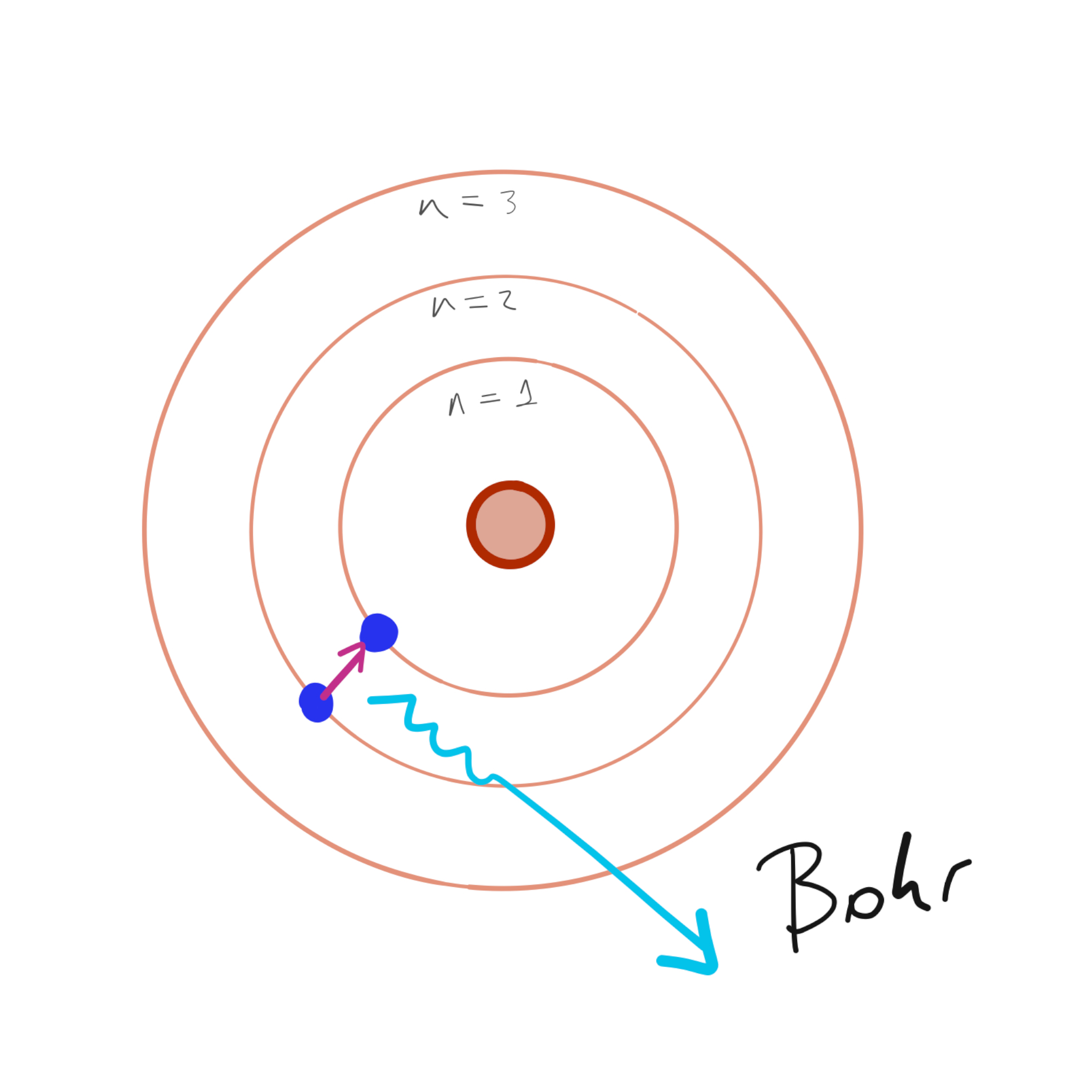
De acuerdo con el modelo atómico de Bohr, los electrones pueden saltar entre niveles identificados con el número entero \(n\) (\(n = 1, 2, 3, ...\)). Cuando un electrón salta de una capa externa a otra interna, debe perder energía, la cual es despedida en forma de fotón. La energía de este fotón será igual a la diferencia energética ente las capas. Al salto de un nivel a otro se lo conoce como «cuanto» haciendo referencia a la propiedad discreta de los valores permitidos. Por su parte también, si la cantidad de electrones de la capa más externa no es la máxima permitida (electrones de valencia), el átomo puede absorber otro \(e^-\) en ella, dando lugar a la interpretación que aún se utiliza para explicar los enlaces químicos.
Modelo de átomo de Schrödinger¶
10 años después que en 1916 Sommerfeld mejorara el modelo atómico de Bohr proponiendo subniveles de energía en los propios niveles energéticos de Bohr, órbitas cuasi-elípticas y velocidades cuasi-relativistas en los \(e^-\), y que todo el sistema giraba en torno al Centro de Masa del mismo (muy cercano al centro del núcleo que contenía la mayor masa), Schrödinger incorpora la ideas de De Broglie y Planck a la interpretación de los átomos.
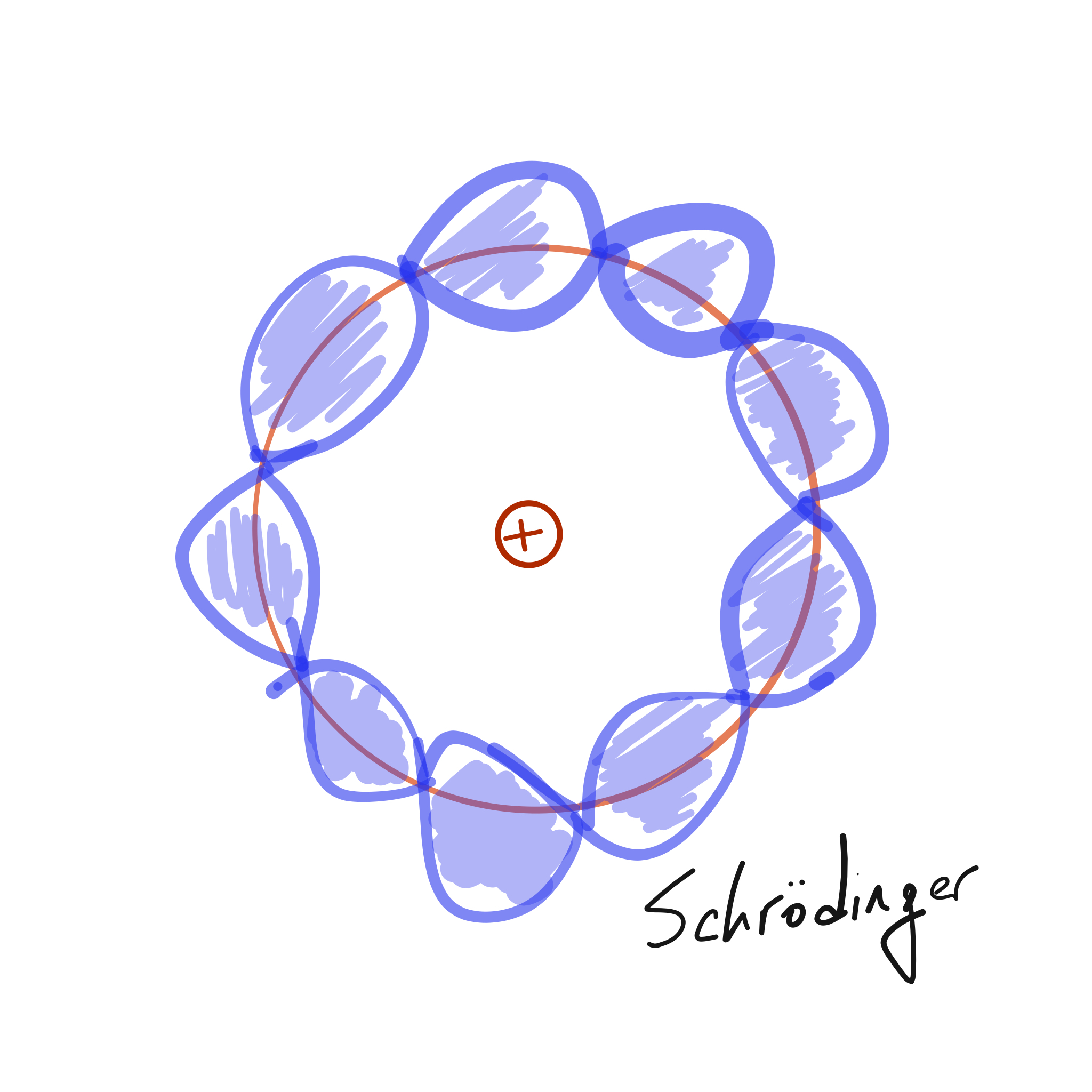
Así, en 1926 Schrödinger presenta su artículo «An undulatory theory of the mechanics of atoms and molecules» en donde describe, entre otros, la importancia de la longitud de onda en problemas de macro y micro mecánica, la ecuación de onda con sus aplicaciones al átomo de hidrógeno, y la razón intrínseca de las frecuencias de características discretas. En este artículo, Schrödinger da nacimiento a lo que se conoce como el modelo mecánico-cuántico del átomo. En este modelo, se describe a los \(e^-\) como cuerpos (materia) definidos por funciones de onda estacionarias. Se deja de pensar en los electrones con posiciones fijas o definidas, tampoco se pretende predecir su ubicación ni describir su desplazamiento. Éste modelo solo establece probabilidades de ubicar al electrón en una zona conocida como orbital.
Tiempo después, Born interpreta la función de onda de Schrödinger determinando que el cuadrado de la amplitud de la función se corresponde con la densidad de probabilidad del estado. Entonces, en esta interpretación derivada de la función de onda el modelo se convierte en probabilístico y es capaz de realizar precisiones empíricas donde la posición y el momento no pueden conocerse en simultáneo por el principio de incertidumbre Heisenberg.
Figura 2: Modelos de átomo de Bohr (izq.) y de Schrödinger (der.).
Las soluciones a la ecuación de Schrödinger se encuentran caracterizadas por los números cuánticos \((n,m,l)\) y en coordenadas esféricas se pueden escribir como
donde \(a_0\) es el radio de Bohr, \(L_{n-l-1}^{2l +1}(\rho)\) son los polinomios de Laguerre generalizados de grado \((n-l-1)\) y \(Y_{l,m}(\theta,\phi)\) es el armónico esférico \((l,m)\). Así, los canales energéticos quedan definidos por
donde \(\alpha\) es la constante de estructura fina y \(\hbar\) la constante de Planck.
Este modelo, aunque avanzado, no tiene en cuenta el espín de los electrones hasta que fue incluido en 1927 por Pauli en su artículo «Sobre la mecánica cuántica del electrón magnético» donde adapta la ecuación en aproximaciones no relativistas. Los efectos relativistas debido a electrones rápidos son posteriormente incorporados en 1928 por Dirac en su artículo «The quantum theory of the electron». Finalmente, la electrodinámica cuántica explica por qué un electrón excitado decae a un nivel inferior cuando existe uno libre.
En el caso particular del átomo de hidrógeno, los aspectos contemplados por el modelo de Schrödinger-Pauli y la ecuación de Dirac pueden corregirse por aproximaciones al hamiltoniano.
La estructura nuclear¶
El modelo introducido por Rutherford y mejorado por Bohr prevé una concentración de la masa del átomo en el núcleo, así como la suma de las cargas positivas. Entonces, el núcleo atómico estaría compuesto por Z protones y (\(\text{A}-\text{Z}\)) neutrones, siendo Z el número atómico y A el número másico o número de masa del átomo. Un núcleo X, en física nuclear, se define entonces por estas cantidades, utilizando la convención \(^A_Z\text{X}\). Así, el núcleo de \(^{60}\text{Co}\) se identifica con el símbolo \(^{60}_{27}\text{Co}\) donde se puede observar que posee 27 protones, 60 - 27 = 33 neutrones y su número másico es 60. Por lo general, el número atómico es omitido, ya que el mismo se encuentra directamente identificado por el símbolo asociado en la tabla periódica. Asimismo, los iones son identificados con el signo positivo o negativo, dando lugar a la expresión \(^4_2\text{He}^{2+}\) que representa un átomo de helio doblemente ionizado, también conocido como partícula \(\alpha\).
Clasificación¶
Teniendo en cuenta los valores relativos Z y A de los núcleos, también se establecen las siguientes convenciones:
un elemento está compuesto por átomos con el mismo número de protones Z. Los átomos con el mismo Z y diferente A son conocidos como isótopos de un determinado elemento.
el término «isótopo» está incorrectamente utilizado para referir a especies nucleares. Así, \(^{12}\text{C}\) y \(^{226}\text{Ra}\) no son isótopos pues no comparten Z y deben ser llamados nucleidos. Por otra parte, el término «radionucleido» refiere solo a las especies radiactivas, aunque el término «radioisótopo» también puede ser utilizado para el mismo propósito.
un nucleido es una especie atómica caracterizada por A, Z y el arreglo de nucleones dentro del núcleo. Isótopo sólo refiere a formas atómicas del mismo elemento químico.
Así, el deuterio y el tritio son isótopos pesados del hidrógeno, el \(^{59}\text{Co}\) y el \(^{60}\text{Co}\) son isótopos del cobalto, y el término nucleido refiere a todas las formas atómicas de todos los elementos.
Los nucleidos pueden ser clasificados en diferentes tipos de grupos. Como vimos, si comparten Z se calsifican como isótopos pero si comparten A se conocen como isóbaros y si comparten neutrones se conocen como isotones. Así, \(^{60}\text{Co}\) y \(^{60}\text{Ni}\) son isóbaros mientras que el tritrio \(^{3}\text{H}\) y el \(^{4}\text{He}\) son isotones con A \(-\) Z=2.
Si un núceo existe en un estado excitado por un tiempo determinado, se dice que se encuentra en un estado isomérico o metaestable. Así, los isómeros son especies nucleares que tienen los mismos Z y A. Por lo tanto, se entiende que el radionucleido \(^{99m}\text{Tc}\) se encuentra en un estado isomérico del \(^{99}\text{Tc}\).
Energía de ligadura nuclear¶
Si sumamos la masa de cada uno de los Z protones y los (\(\text{A} - \text{Z}\)) neutrones que componen el núcleo atómico y la comparamos con la masa del núcleo, encontraremos que la primera es diferente a la segunda. La diferencia entre éstas, \(\Delta \text{m}\), es conocida como defecto de masa y su equivalente energético, \(\Delta \text{mc}^2\), es conocido como la energía de ligadura \(\text{E}_\text{B}\) del núcleo. \(\text{E}_\text{B}\) es, entonces, la energía que debe ser liberada para lograr unir los nucleones.
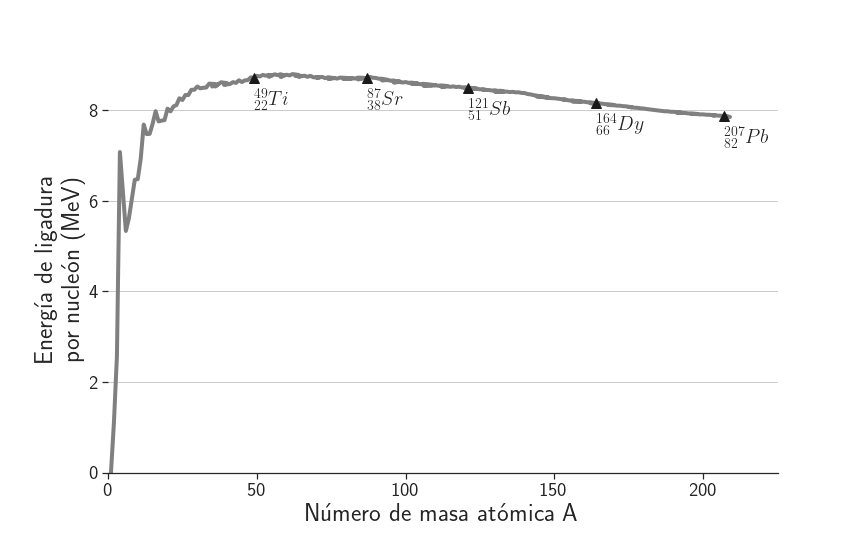
La energía de ligadura por nucleón, \(\text{E}_\text{B}/\text{A}\), si bien varía con A se mantiene en el orden de los ~8 MeV/nucleón a partir de \(\text{A} \approx \text{30}\) y alcanza un máximo en torno a \(\text{A} \approx \text{60}\), como se muestra en la Figura 3. A mayor \(\text{E}_\text{B}/\text{A}\), mayor será la estabilidad del átomo pues mayor será la energía necesaria para separar sus nucleones.
Figura 3: Energía de ligadura por nucleón.
Radio nuclear¶
El radio R de un núcleo se estima a partir del número másico por medio de la fórmula
donde \(\text{R}_\text{0}\) = 1,25 fm = 1,25 \(\times \text{10}^{-\text{15}}\) m. Como A puede variar entre 1 y 250, entonces el radio de los diferentes núcleos se encuentra en un rango de entre 1 fm y 8 fm. Esta aproximación, de todas formas, es más exacta para los núcleos «esféricos», es decir con A bajo.
Tamaño del núcleo derivado de la energía de ligadura¶
La existencia misma de los núcleos es evidencia de que la fuerza nuclear fuerte es capaz de contrarrestar la repulsión coulombiana de los protones. La fuerza nuclear fuerte es una de las cinco fuerzas fundamentales establecidas por el modelo estándar en física de partículas. Estas fuerzas, no resultan perceptibles más allá del fm de distancia. Como la fuerza de atracción entre nucleones es prácticamente la misma entre sus distintas configuraciones (protón-protón, protón-neutrón y neutrón-neutrón), las diferencias que puedan existir entre las energías de ligadura entre núcleos con misma cantidad de nucleones (mismo A) se debe a la energía coulombiana de los protones. Por ejemplo, el \(^3\text{He}\) posee energía de ligadura de \(\approx\) 8,5 MeV, mientras que el \(^3\text{H}\) tiene \(E_\text{B}\) de \(\approx\) 7,7 MeV. Al tener el \(^3\text{He}\) más protones, necesita más \(E_\text{B}\) para compensar esta repulsión eléctrica.
El potencial Coulombiano de un núcleo esférico de radio \(\text{R}_\text{N}\) y carga eléctrica \(\text{Z}\cdot\text{e}\) uniformemente distrbuida en su interior es
Ahora, asumiendo que el volumen nuclear escala linealmente con el número de nucleones, el radio nuclear deberá ser proporcional a \(\sqrt[3]{A}\) (como se mostró antes). Entonces, el radio debe ser el mismo para \(^3\text{He}\) y para \(^3\text{H}\) y puede ser calculado directamente de la diferencia de \(\text{E}_\text{Coul}\)
de donde podemos obtener un radio de 3,4 fm para estos núcleos.
Fusión y fisión nuclear¶
La forma particular de la curva de \(\text{E}_\text{B}/\text{A}\) vs. A sugiere dos métodos para convertir masa en energía: fusión, en el caso de los núcleos de bajo número másico A; y fisión en el caso de los núcleos de alto número de masa atómico. El valor máximo para \(\text{E}_\text{B}/\text{A}\) en la figura anterior es de ~8,79 MeV/nucleón, por lo que podemos dividir la gráfica anterior como se muestra en la Figura 4, definiendo éste como el punto de corte, ubicando a la derecha los núcleos que permitirían obtener energía por método de fisión y a la izquierda aquellos propensos a permitir la generación de energía a partir de la fusión nuclear.
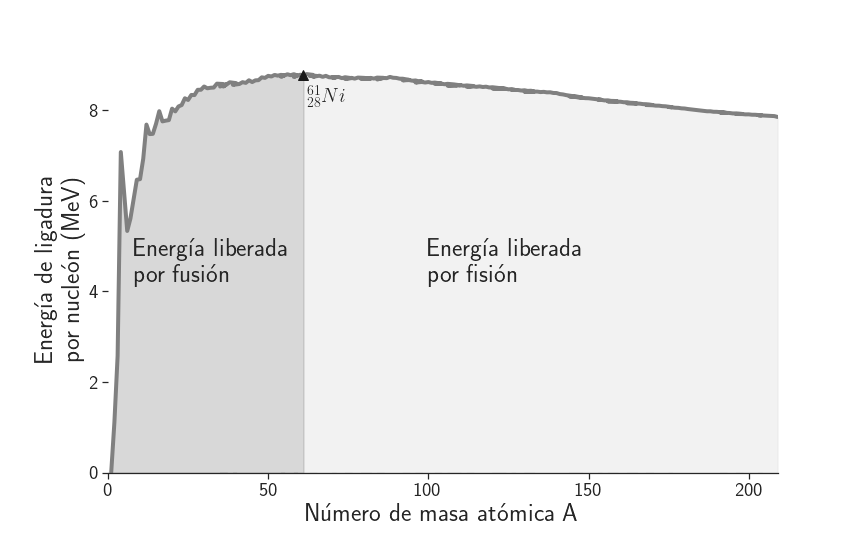
Figura 4: Energía de ligadura por nucleón .
Fusión¶
La fusión de dos núcleos de masas pequeñas (A < 60), creará un nucleo más masivo, liberando energía en el proceso. Éstos núcleos «livianos» (A menor que para Ni, Co o Fe donde se alcanzan las mayores energías de ligadura por nucleón), al unirse dos o más de ellos, generalmente liberan energía. En el caso más simple, cuando se unen dos protones, debe invertirse una energía que venza la repulsión eléctrica entre ambos, tal que se acerquen lo suficiente como para permitir la interacción nuclear fuerte y generar así la liberación de energía en su fusión. Entonces, la unión de un deuterio (\(^2\text{H}\)) y un tritio (\(^3\text{H}\)) genera helio (\(^4\text{He}\)), libera un neutrón y 17,59 MeV de energía.
En 1919, Rutherford logró lo que soñaron por siglos los alquimistas, convirtió por primera vez en la historia un elemento químico en otro de forma artificial. El fenómeno de transmutación sucedió al bombardear un átomo de nitrógeno con partículas \(\alpha\). Desde hace más de 4 siglos se sabe que el plomo y el oro poseen densidad semejante, lo que llevó a alquimistas durante siglos a pretender convertir uno en el otro por medio de reacciones químicas, hasta que Lavoisier dió inicio a la química moderna con su ley de conservación de la materia. Desde Rutherford sabemos que el átomo posee núcleo, y que no es posible convertir un elemento en otro a través de reacciones químicas, ya que éstas solo se dan por interacción de los electrones de las capas exteriores. En cambio, para convertir un elemento en otro es necesario modificar la cantidad de protones. Convertir plomo (Z=82) en oro (Z=79) implica poder extraerle 3 protones al núcleo de plomo. Hacerlo es posible y se ha realizado, pero la energía necesaria para extraer 3 protones del plomo es tan grande y el esfuerzo tecnológico es tan costoso que resulta infinitamente más económico comprar el oro en el mercado.
Siguendo los estudios de Rutherford, Mark Oliphant logró en 1932 la primera fusión de dos núcleos ligeros (isótopos de hidrógeno), investigaciones que continuó Hans Bethe por más de 10 años. Estudios militares y civiles que intentan la fusión nuclear controlada llevan más de 70 años. Aunque se ha logrado, aún no ha sido controlada completamente. En la naturaleza, la fusión se da naturalmente en las estrellas a temperaturas cercanas a los 15 millones de grados Kelvin.
Existen varias ventajas de la fusión respecto de la fisión que justifican los esfuerzos tecnológicos realizados en los últimos 70 años. La fusión se realiza con elementos livianos, como el deuterio (presente en el agua del mar) y el tritio, que puede generarse fácilmente gracias al neutrón liberado en la unión \(^2\text{H}\) + \(^3\text{H}\). Por esto, los combustibles para la fusión son económicos y abundantes, posibilitando la generación de energía por millones de años. Además, de lograrse de forma controlada, es un sistema seguro, ya que la reacción no es en cadena y se termina instantáneamente al dejar de entregar combustible al sistema. Cabe destacar que esta tecnología, no produce residuos nocivos (produce He) y la estructura de los reactores solo debe preservarse por 50 años, ya que solo deben considerarse materiales necesarios para blindar la generación de neutrones.
Existen distintos tipos de técnicas para lograr la fusión nuclear. La primera e intuitiva es la que utiliza aceleradores para entregar energía a los núcleos, de forma tal que venzan la repulsión eléctrica. Éste tipo de tecnología, si bien logra el objetivo, es completamente ineficiente, ya que necesita más energía para lograr la fusión que la liberada por los nucleones al unirse. Entre las alternatias, se encuentra la técnica de confinamiento inercial, que utiliza láseres para comprimir esferas de combustible obteniendo densidades elevadas y logrando la fusión por efecto túnel gracias a la cercanía de los núcleos. Otra técnica, que también utiliza el efecto túnel para la fusión de núcleos, es la de confinamiento magnético donde el combustible se calienta a temperaturas de millones de grados generando choques por agitación térmica. En esta última, al alcanzar tan altas temperaturas, el combustible se disocia entre cargas positivas y negativas, pudiendo ser controlado por campos magnéticos.
Fisión¶
A diferencia de la fusión, la fisión consiste en separar nucleones, lo que se logra bombardeando elementos de alto A como el \(^{235}\text{U}\) con neutrones térmicos en un reactor nuclear. Esto genera dos elementos de menor masa, más estables, y libera energía cinética.
Al igual que los experimentos de fusión, las investigaciones experimentales sobre fisión datan de fines de los 30 y principios de los 40 del siglo pasado. En 1938, Otto Hann <https://es.wikipedia.org/wiki/Otto_Hahn> descubre la fisión (lo que le vale el Nobel de Química en 1944). En 1942 Fermi logra la primera reacción en cadena controlada basada en fisión nuclear y, desde entonces, los reactores nucleares basados en fisión se han convertido en una de las principales fuentes de energía eléctrica.
Para elementos de A menores a Fe, Ni o Co, la fisión nuclear implica la entrega de energía, mientras que para elementos con A > 60 la fisión libera energía. Cuanto más másico es el núcleo de un átomo, más propenso será a la fisión. Por esto, para los reactores de fisión nuclear se utilizan elementos de muy alto A, como el ^{235}text{U}.
Al fisionar, el nucleido genera otros nucleidos de menor A y otro tipo de partículas. Por ejemplo, el ^{235}text{U} genera elementos de A entre 72 y 160, la mayoría radiactivos que se desintegran emitiendo electrones por exceso de neutrones, dando lugar a una reacción en cadena que genera más de 200 especies radiactivas distintas.
La fisión es la reacción utilizada en las centrales nucleares de todo el mundo, no emite gases que generan efecto invernadero y, de almacenarse correctamente sus residuos, es la única energía capaz de abastecer ciudades sin contaminar. La cuestión de los residuos, así como la de la seguridad, son centrales en la operación de estas centrales. Ambas cuestiones se encuentran resueltas técnicamente y guiadas por controles internacionales severos, lo cual despeja viejos mitos y dudas generados en décadas pasadas.
Reacciones nucleares¶
La colisión entre dos partículas se clasifica en 3 categorías: dispersión elástica, colisión inelástica y reacción nuclear. En el primer caso, el producto de la interacción es idéntico a las partículas antes de la misma. Se conserva el momento y la energía cinética. En el segundo caso, al igual que en la dispersión elástica, las partículas producto son idénticas pero en este caso la partícula proyectil transmite energía a la partícula blanco no solo en forma de energía cinética (puede ser excitando), generando un cambio en el momento y la energía cinética total del sistema final. En cambio, en una reacción nuclear, los productos de la reacción son diferentes a las partículas/núcleos que reaccionaron antes. Estos productos tienen otro número atómico, y se deben conservar ciertas cantidades como carga, momento lineal y masa-energía. Además, la suma de Z y A antes y después de la reacción se debe mantener.
Llamaremos reacciones nucleares a las interacciones entre núcleos atómicos o entre núcleos y partículas elementales. Aunque el término también comprende a las interacciones entre partículas elementales entre sí. La primera de estas fue lograda por Rutherford en 1919, bombardeando el isótopo de nitrógeno \(^14_7\text{N}\) con partículas alfa, generando un \(^17_8\text{O}\) y un protón, como se muestra en la ecuación
La radiactividad, así, es la reacción nuclear más simple y espontánea. En el resto de los casos, se involucran dos o más núcleos y/o partículas generando productos de la reacción.
El valor Q de una reacción nuclear se define por la diferencia entre la energía total en reposo antes de la reacción y la final. Si interactúan una partícula \(m_1\) y otra \(m_2\) produciendo otras dos partículas \(m_3\) y \(m_4\), Q resulta:
Las reacciones con Q>0 son denominadas exotérmicas y liberan energía, las reacciones con Q<0 son denominadas endotérmicas y requieren entrega de energía del proyectil al blanco, mientras que las reacciones con Q=0 son denominadas elásticas. Las reacciones exotérmicas pueden ocurrir espontáneamente, mientras que las endotérmicas solo ocurren cuando el proyectil supera una energía de corte \((\text{E}_\text{k})_\text{th}\) determinada por:
donde \(m_1\) es el proyectil, \(m_2\) el blanco, y \(m_3\) y \(m_4\) son los productos de la reacción.