


Next: Un extremo fijo y
Up: La Cuerda Elástica:
Previous: La Cuerda Elástica:
Si ambos extremos están fijos (cuerda atada), las condiciones
en el contorno pueden escribirse de la siguiente manera:
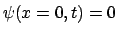 y
y
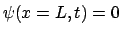 . La primera de estas
condiciones queda satisfecha de forma automática por la
Ec. (7) dado que habiamos elegido una función seno
para el perfil de las ondas viajeras.
La segunda condición impone por otro lado que
. La primera de estas
condiciones queda satisfecha de forma automática por la
Ec. (7) dado que habiamos elegido una función seno
para el perfil de las ondas viajeras.
La segunda condición impone por otro lado que
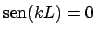 . De lo cual tenemos que los posibles
valores de
. De lo cual tenemos que los posibles
valores de 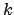 son
son
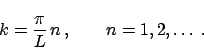 |
(8) |
Por lo tanto los posibles valores de 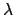 resultan
resultan
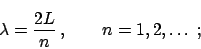 |
(9) |
y a partir de la Ec. (4) tenemos que las posibles
frecuencias de oscilaciones estacionarias son
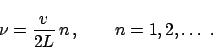 |
(10) |
Las sucesivas frecuencias resultan así multiplos enteros
de la frecuencia fundamental (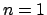 ).
Es importante notar que en las oscilaciones estacionarias armónicas
(
).
Es importante notar que en las oscilaciones estacionarias armónicas
(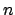 fijo), tambien conocidas como modos normales de
oscilación, los puntos de la cuerda cuyas coordenadas son
fijo), tambien conocidas como modos normales de
oscilación, los puntos de la cuerda cuyas coordenadas son
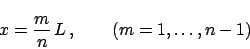 |
(11) |
permanecen en reposo durante las oscilaciones (además de
los extermos). Estos puntos se conocen como nodos de la
oscilación.



Next: Un extremo fijo y
Up: La Cuerda Elástica:
Previous: La Cuerda Elástica:
Pedro Pury
2005-03-09
![]() y
y
![]() . La primera de estas
condiciones queda satisfecha de forma automática por la
Ec. (7) dado que habiamos elegido una función seno
para el perfil de las ondas viajeras.
La segunda condición impone por otro lado que
. La primera de estas
condiciones queda satisfecha de forma automática por la
Ec. (7) dado que habiamos elegido una función seno
para el perfil de las ondas viajeras.
La segunda condición impone por otro lado que
![]() . De lo cual tenemos que los posibles
valores de
. De lo cual tenemos que los posibles
valores de ![]() son
son