Si un sólo extremo está fijo y el otro se encuentra libre,
las condiciones en el contorno pueden escribirse según:
![]() y
y
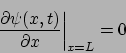 |
(12) |
Ejercicios
(para realizar antes de entrar al laboratorio):
1) Calcular las posiciones de los nodos en los modos normales de oscilación de la cuerda con un extremo libre.
2) Graficar los patrones espaciales de los cuatro primeros modos normales para la cuerda con:
a) ambos extremos fijos,
b) un solo extremo fijo.
Por último, para cada medio elástico existe una relación
constitutiva que vincula la velocidad de propagación con las
características del medio en cuestión. Para una cuerda
elástica, en particular, puede demostrarse que