Desarrollo Experimental:

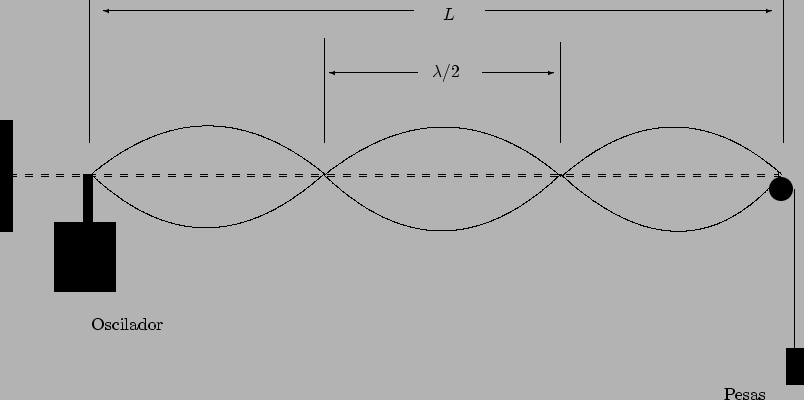
En la Figura de describe esquemáticamente el dispositivo experimental con el que se trabaja para el caso de la cuerda fija en ambos extremos. La longitud de la cuerda $L$ se mide desde el punto en el cual esta fija al oscilador y hasta el punto de contacto con la polea en el otro extremo.

El oscilador es de frecuencia variable $\nu$ y la tensión $T$ de la cuerda es regulada mediante las pesas que se cuelgan del extremo libre. Es importante evaluar adecuadamente las apreciaciones con las cuales pueden determinarse $\nu$ y $T$.

Experiencia 1: Tensar la cuerda de aproximadamente $1,5\,$m de longitud con una valor próximo a $T = 2,5\,$N. Barrer en frecuencia $\nu$ para encontrar los sucesivos modos normales de oscilación. Contar para cada caso el número de nodos $m$ obtenido y así calcular el orden $n = m+1$ del correspondiente modo normal. A partir de las Ec. (10) y (16) se tiene que

$$\nu^2 = \frac{T}{4 L^2 \mu} \,n^2 \;.$$ (17)

Realizar un ajuste lineal de esta relación para calcular la densidad de masa $\mu$ de la cuerda.

Experiencia 2: Fijar un valor de frecuencia próximo a $\nu = 10\,$Hz. Variar la tensión $T$ para encontrar los sucesivos modos normales de oscilación y contar nuevamente para cada caso el número de nodos $m$ obtenido. A partir de la Ec.(17), realizar un ajuste lineal para calcular la densidad de masa $\mu$ de la cuerda.

Experiencia 3: Para simular la condición de contorno libre, atar la cuerda a un trozo de alambre rígido de unos 25 cm de longitud y trabajar con 90 cm de cuerda tensada aproximadamente a 2,5 N. Barrer en frecuencia $\nu$ para encontrar los sucesivos modos normales de oscilación. A partir de un adecuado ajuste lineal calcular la densidad de masa $\mu$ de la cuerda.

Experiencia 4: Montar la cuerda entre dos sensores de fuerza digitales, utilizando una tensión menor a 10 N. Punzar la cuerda en un extremo muy próximo a uno de los sensores y medir el tiempo que tarda el pulso en llegar al otro extremo de la cuerda. Calcular así la velocidad de propagación del pulso.

Experiencia 5: Retirar la cuerda y proceder a la determicación de la densidad de masa $\mu$ por medio de una cinta métrica y una balanza de precisión. Evaluar como cambia la densidad de masa con la tensión a la que es sometida la cuerda. Comparar el valor obtenido con el de las experiencias anteriores. Calcular utilizando la Ec. (16) la velocidad de propagación bajo la tensión utilizada en la experiencia inmediata anterior. Comparar los valores obtenidos en ambas experiencias identificando en cada caso la fuente principal de incerteza.

Bibliografía:

• U. Ingard y W. L. Kraushaar, Introducción al Estudio de la Mecánica, Materia y Ondas, Reverté, Barcelona (1973); Cap. 23.

• J. S. Fernández y E. E. Galloni, Trabajos Prácticos de Física, La Linea Recta, Buenos Aires (1963); Cap. IV.

Fa.M.A.F ©2005