Reacciones químicas

En un sistema gaseoso multicomponente las reacciones químicas ocurren cuando los distintos tipos de moléculas pueden transformarse unos en otros mediante colisiones inelásticas. Para que ocurra una reacción las moléculas deben poseer energía suficiente como para superar las barreras de potencial que existan. El estado de equilibrio químico es estacionario a nivel macroscópico, pero dinámico a nivel molecular, ya que la reacción no se detiene.

Un avance importante para la descripción de las reacciones químicas ha sido introducido por de Donder a principios del siglo XX: es posible caracterizar una reacción química mediante una sola variable $\xi$, como veremos a continuación. Para ello consideremos la reacción

$$-\nu_A A - \nu_B B \rightleftharpoons \nu_C C + \nu_D D \;.$$

Como dijimos en la sección , $A,B,C$ y $D$ (y en general $A_j$) se denominan componentes químicos y los parámetros $\nu_j$, coeficientes estequiométricos. En la notación introducida aquí, $\nu_A$ y $\nu_B$ son negativos.

Supongamos que inicialmente $n_A=-\nu_A n_o$ moles, $n_C=\nu_C n_o'$, $n_B=-\nu_B n_o + N_B$ y $n_D=\nu_D n_o' + N_D$. La reacción se ``completa'' hacia la derecha cuando

$$n_A=0\;, \qquad n_B=N_B\;, \qquad n_C=\nu_C(n_o+n_o') \qquad {\rm y} \qquad n_D=\nu_D(n_o+n_o')+N_D \;.$$

Hacia la izquierda la reacción se completa cuando

$$n_A=-\nu_A(n_o+n_o')\;, \qquad n_B=-\nu_B(n_o+n_o')+N_B\;, \qquad n_C=0 \qquad {\rm y} \qquad n_D=N_D \;.$$

Definimos entonces el grado de reacción como

$$\xi = (n_o+n_o') + \frac{n_A}{\nu_A} \qquad\qquad 0\leq\xi\leq n_o+n_o' \;.$$

Vemos que $\xi$ mide números de moles, y que nos permite escribir

$$\begin{array}{rcl} n_A &=& -\nu_A(n_o+n_o') + \nu_A \xi ... ... \\ n_C &=& \nu_C \xi\\ n_D &=& N_D + \nu_D \xi \end{array}$$ (7)

Hemos expresado entonces todos los números de moles $n_j$ en cualquier paso intermedio de la reacción en términos solamente de la variable $\xi$. Cualquier cambio en las concentraciones del sistema se puede resumir como ${\rm d}n_j = \nu_j {\rm d}\xi$, o bien

$$\frac{ {\rm d}n_A}{\nu_A} = \frac{ {\rm d}n_B}{\nu_B} = \... ...d}n_C}{\nu_C} = \frac{ {\rm d}n_D}{\nu_D} = {\rm d}\xi \;.$$

En otros términos, los cambios en las propiedades termodinámicas del sistema se representan mediante una única variable.

Típicamente en una reacción se controlan $T$ y $P$. Éstas son las variables naturales de la energía libre de Gibbs, de modo que intentaremos encontrar las condiciones para el equilibrio aplicando el principio de mínimo para este potencial. A partir de la definición $G=U-TS+PV$, podemos recordar la relación de Euler para escribir

$$G = \sum_j \mu_j n_j \;.$$

Para un sistema simple, el potencial de Gibbs molar coincide con el potencial químico

$$\frac{G}{n} = \mu \;,$$

mientras que para un sistema multicomponente,

$$\frac{G}{n} = \sum_j \mu_j x_j \;,$$

donde $x_j\equiv n_j/n$ es la fracción molar del componente $j$. Queremos estudiar las variaciones diferenciales de $G$ cuando $T$ y $P$ se mantienen constantes:

$${\rm d}G = \sum_{j=1}^r \mu_j {\rm d}n_j = \sum_{j=1}^r \mu_j \nu_j {\rm d}\xi \;,$$

o bien

$$\left(\frac{\partial G}{\partial\xi}\right)_{T,P} = \sum_{j=1}^r\mu_j\nu_j \equiv {\cal A} \;.$$

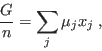
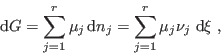
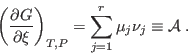
En el equilibrio, $G$ debe ser mínimo, de modo que la afinidad $\cal A$ debe anularse para cierto $\xi_{\rm eq}$. En realidad, si en un sistema cerrado $T$ y $P$ se mantienen constantes y las variaciones de todos los $\{n_j\}$ se representan en términos de la variable $\xi$, los valores del potencial de Gibbs sólo pueden depender de esa única variable: $G(\xi)$ entonces debe semejarse a una parábola como se muestra en la figura. Si la reacción está moviéndose al equilibrio desde la izquierda ${\cal A}<0$, mientras que si se aproxima desde la derecha, ${\cal A}>0$.

 

Como la entalpía está vinculada con el potencial de Gibbs mediante la relación $H=G+TS$, y en virtud de que ahora consideramos como variables independientes a $T$, $P$ y $\xi$, podemos escribir

$$\left(\frac{\partial H}{\partial\xi}\right)_{T,P} = \left(... ...,P} + T \left(\frac{\partial S}{\partial\xi}\right)_{T,P} \;.$$

Puesto que en el equilibrio el primer término de la derecha es cero, esta identidad nos dice que los cambios en la entalpía durante la reacción son proporcionales a los flujos de calor hacia el sistema. Por este motivo la derivada $(\partial H/\partial\xi)_{T,P}$ se denomina calor de reacción y representa el calor absorbido por el sistema ``por unidad de reacción'' alrededor del equilibrio. Si esta cantidad es positiva, la reacción es endotérmica, mientras que si es negativa, se dice que la reacción es exotérmica.

Considerando que

$$S = - \left(\frac{\partial G}{\partial T}\right)_{P,\{n_j\}} = - \left(\frac{\partial G}{\partial T}\right)_{P,\xi}$$

y teniendo la precaución de que $\xi$ es otra variable independiente para $G$, se obtiene

$$\left(\frac{\partial H}{\partial\xi}\right)_{T,P} = -T \fra... ...ac{\partial }{\partial T} \left(\sum_{j=1}^r\mu_j\nu_j\right)$$

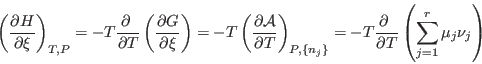
Para el caso concreto de una mezcla de gases ideales (o de una mezcla en la que los $\mu_j$ se comportan como los de gases ideales), podemos escribir una expresión cerrada para la afinidad a partir de la expresión correspondiente a la energía libre de Gibbs molar: se deja como ejercicio verificar que la contribución de la componente $j$ es $\mu_j=RT[\phi_j(T)+\ln P+\ln x_j]$, resultando para la afinidad

$$\begin{eqnarray*} {\cal A} &=& \sum_{j=A}^D \mu_j\nu_j \;=\; \sum \nu_j RT \le... ...^{\nu_C}x_D^{\nu_D}}{x_A^{\vert\nu_A\vert}x_B^{\vert\nu_B\vert}} \end{eqnarray*}$$

(recordemos que $\nu_A$ y $\nu_B$ son negativos). De esta expresión puede verse que la afinidad tiende a $-\infty$ a medida que $\xi\to 0$ y a $+\infty$ cuando $\xi\to n_o+n_o'$, tal como habíamos indicado en el gráfico de anterior.

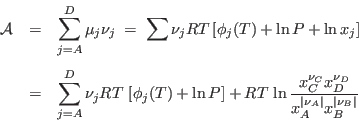
Para un sistema en equilibrio químico a $T$ y $P$ fijos, vemos que el cociente $x_C^{\nu_C}x_D^{\nu_D}/(x_A^{\vert\nu_A\vert}x_B^{\vert\nu_B\vert})$ está completamente determinado por los valores de $T$ y $P$, ya que $\cal A$ debe anularse. Una forma alternativa de expresar la condición anterior para el equilibrio es

$$\ln \left[\frac{x_C^{\nu_C}x_D^{\nu_D}}{x_A^{\vert\nu_A\ver... ...u_B\vert}} P^{\nu_C+\nu_D+\nu_A+\nu_B}\right] = \ln K(T) \;,$$

donde $\ln K(T)\equiv-\sum_j\nu_j\phi_j(T)$ sólo depende de $T$. Este resultado se conoce con el nombre de ley de acción de masas. Suele tabularse $K(T)$ para cada reacción, de modo que para cada $T$ y $P$ puede conocerse el conjunto de fracciones molares si se tienen como datos los $\{n_j\}$ iniciales, utilizando las relaciones ().