Siguiente: Gas de Fermi-Dirac Subir: clases-t2 Anterior: PartÝculas de Maxwell-Boltzmann
Hemos visto que la gran partición para un sistema de partículas regido por la estadística de Bose-Einstein está dada por la ecuación (19), la que puede reescribirse como
![$\displaystyle Z_\mu^{\rm (BE)}(T,V) = \prod_{\ell'=0}^\infty \left[
\sum_{n_{\ell'}=0}^\infty e^{-\beta(\epsilon_{\ell'}-\mu)n_{\ell'}}
\right] \;,
$](img862.png)
![$\displaystyle Z_\mu^{\rm (BE)}(T,V) = \prod_{\ell'=0}^\infty\;
\left[ \frac{1}{1-e^{-\beta(\epsilon_{\ell'}-\mu)}} \right] \;.
$](img865.png)
![$\displaystyle Z_\mu^{\rm (BE)}(T,V) = \prod_{\ell=0}^\infty\;
\left[ \frac{1}{1-e^{-\beta(\epsilon_\ell-\mu)}} \right]^{g_s} \;.
$](img873.png)
De aquí en adelante trataremos el caso de partículas sin espín (![]() ),
aunque la generalización para
),
aunque la generalización para ![]() es directa. Obtenemos entonces para
el gran potencial
es directa. Obtenemos entonces para
el gran potencial
![$\displaystyle \Omega_{\rm BE}(T,V,\mu) = kT \sum_{\ell=0}^\infty\;
\ln \left[ 1-e^{-\beta(\epsilon_\ell-\mu)} \right] \;,
$](img876.png)
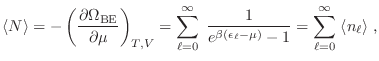
En particular, vemos que la población del estado fundamental
Podemos reescribir las expresiones para el gran potencial y el número medio
de partículas tomando el límite termodinámico, de manera que convertimos las
sumatorias en integrales siguiendo el procedimiento habitual, en términos del impulso lineal ![]() o de la energía individual
o de la energía individual
![]()
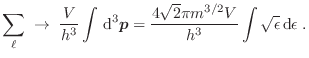
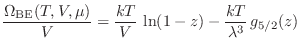
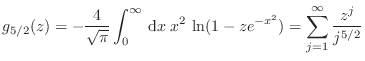
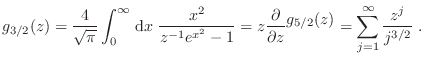
|
A estas expresiones integrales se arriba realizando la sustitución
|
|
estado
![]() deja de ser “diferencial” para poblarse macroscópicamente: de esta manera, en el límite termodinámico (
deja de ser “diferencial” para poblarse macroscópicamente: de esta manera, en el límite termodinámico (
![]() ), el cociente
), el cociente
![]() . Este es el verdadero motivo por el cual se separan las contribuciones correspondientes a
. Este es el verdadero motivo por el cual se separan las contribuciones correspondientes a
![]() en las expresiones anteriores. La población macroscópica del estado con impulso cero se conoce como condensación de Bose-Einstein, y en seguida veremos que se corresponde con una transición de fase.
en las expresiones anteriores. La población macroscópica del estado con impulso cero se conoce como condensación de Bose-Einstein, y en seguida veremos que se corresponde con una transición de fase.
|
La expresión (21) debe entonces desdoblarse para distinguir las situaciones mencionadas, de manera que tendremos
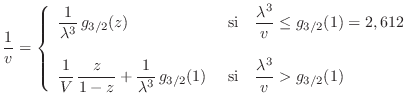
Dicho de otro modo, el valor de la fugacidad se obtiene según qué caso corresponda:
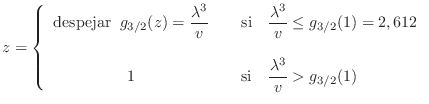
|
|
Para una dada densidad ![]() , hay una temperatura crítica
, hay una temperatura crítica ![]() a
la cual ocurre el cambio, y está dada por
a
la cual ocurre el cambio, y está dada por
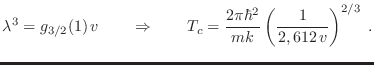
Del mismo modo, para una dada ![]() , el volumen específico crítico
resulta
, el volumen específico crítico
resulta
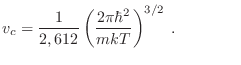
|
De las expresiones anteriores puede obtenerse la fracción de partículas en
el estado
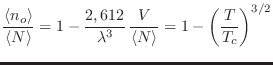
En virtud de la ecuación de Euler
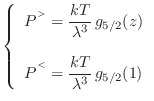
donde hemos indicado con un supraíndice “
Las isotermas en un diagrama
|
|
líquido-gas, la región horizontal puede pensarse como una región de coexistencia: alguna inestabilidad ha sido subsanada en el potencial de Helmholtz uniendo dos estados mediante una recta, cuya pendiente (constante) corresponde al valor de la presión en la coexistencia.
La presión de vapor representada por la curva cortada de la figura, está dada por la condición
![$\displaystyle P_o(T) = \frac{kT}{\lambda^3} g_{5/2}(1) \quad \textcolor{gris}...
... g_{5/2}(1)}{m\left[g_{3/2}(1)\right]^{5/3}} \frac{1}{v_c^{5/3}}
\right)} \;.
$](img923.png)
![$\displaystyle \frac{ {\rm d}P_o}{ {\rm d}T} = \frac52 \frac{k g_{5/2}(1)}{\...
... =
\frac 1{T v_c} \left[\frac52 kT \frac{g_{5/2}(1)}{g_{3/2}(1)}\right] \;.
$](img925.png)
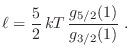
Para el potencial de Gibbs se obtiene
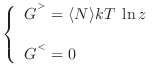
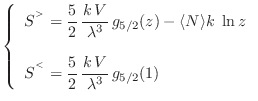
Combinando las ecuaciones anteriores encontramos la energía interna
|
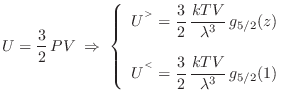
Podemos calcular de aquí el calor específico (por partícula) a volumen
constante, tomando la precaución de derivar la entropía manteniendo
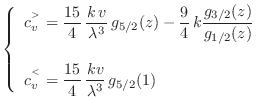
|
|
El aspecto de la curva de ![]() ha hecho que este cambio de fase
se denomine “transición lambda”.
ha hecho que este cambio de fase
se denomine “transición lambda”.
Como habrá notado el avezado lector, hemos recurrido a la ecuación (21) para ![]() o a la anterior para
o a la anterior para
![]() , incluyendo o despreciando la contribución de las partículas en el estado con
, incluyendo o despreciando la contribución de las partículas en el estado con ![]() , según nuestra conveniencia. Sin embargo, puede demostrarse que siempre puede incluirse esta contribución sin que pierdan validez los resultados encontrados. Se sugiere como ejercicio realizar esta verificación.
, según nuestra conveniencia. Sin embargo, puede demostrarse que siempre puede incluirse esta contribución sin que pierdan validez los resultados encontrados. Se sugiere como ejercicio realizar esta verificación.
Para el caso de un gas de fotones, como el número de partículas no se conserva, la maximización de la entropía estadística no conlleva el vínculo asociado con
![]() , de manera que no aparece el correspondiente multiplicador de Lagrange, y las poblaciones de los estados
, de manera que no aparece el correspondiente multiplicador de Lagrange, y las poblaciones de los estados
![]() toman la forma
toman la forma
![]() en lugar de
en lugar de
![]() . Esto es equivalente a aceptar que para fotones
. Esto es equivalente a aceptar que para fotones ![]() , y está claro que en este caso el gran potencial
, y está claro que en este caso el gran potencial ![]() coincidirá con la energía libre de Helmholtz
coincidirá con la energía libre de Helmholtz ![]() . El hecho de que el potencial químico se anule en este caso, podría esperarse de antemano aceptando que ocurre una “reacción química” en las paredes de la cavidad, en la que el intercambio de energía de la radiación con las mismas implica la creación o absorción de fotones. La gran partición que se obtiene de este modo coincide con la partición correspondiente al sistema de osciladores de frecuencias respectivas
. El hecho de que el potencial químico se anule en este caso, podría esperarse de antemano aceptando que ocurre una “reacción química” en las paredes de la cavidad, en la que el intercambio de energía de la radiación con las mismas implica la creación o absorción de fotones. La gran partición que se obtiene de este modo coincide con la partición correspondiente al sistema de osciladores de frecuencias respectivas
![]() : en ese caso, cada oscilador se encuentra en el estado cuántico
: en ese caso, cada oscilador se encuentra en el estado cuántico ![]() , en lugar de pensar que el modo electromagnético de frecuencia
, en lugar de pensar que el modo electromagnético de frecuencia
![]() posee un número variable de fotones
posee un número variable de fotones ![]() .
.
Gustavo Castellano 19/11/2021