Siguiente: Partículas y muestras rugosas Subir: Microanálisis con sonda de Anterior: Distribución de ionizaciones

Intensidad de rayos x emitidos

A partir de la distribución de ionizaciones de un elemento $i$ puede obtenerse la intensidad de rayos x primarios generada en la muestra como la suma de las contribuciones correspondientes a las diferentes capas en las que se divide el material

$$G_i = \sum_j \phi_i(\rho z_j) \Delta I_i^o \;.$$

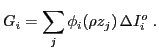
Introduciendo el número de ionizaciones $n_i^o$ generadas en una capa aislada de espesor másico unitario

$$\Delta I_i^o = n_i^o \Delta(\rho z) \;,$$

y pensando en el proceso de límite correspondiente a $\Delta(\rho z)\to0$ , podemos escribir

$$G_i = n_i^o \int_0^\infty {\rm d}(\rho z) \phi_i(\rho z) \;.$$

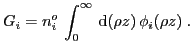
Del mismo modo, la intensidad primaria que emerge de la muestra, y que corresponde a la que se detecta experimentalmente, debe computarse como la suma de las contribuciones provenientes de cada capa sumergida a una profundidad $z_j$ :

$$I_i = \sum_j\phi_i(\rho z_j) e^{-\mu(E_i)\rho z_j \cosec\psi}\D... ...\infty {\rm d}(\rho z) \phi_i(\rho z) e^{-\mu(E_i)\rho z \cosec\psi} \;.$$ (4)

Con estos elementos, y definiendo $\chi_i\equiv\mu(E_i)\cosec\psi$ , podemos calcular la fracción de radiación detectada como

$$f(\chi_i) \equiv \frac{I_i}{G_i} = \frac{\int_0^\infty {\rm d}(... ...}}{\int_0^\infty {\rm d}(\rho z) \phi_i(\rho z)}\;.\rule[-1.5em]{0em}{1em}$$

El lector puede verificar que para el caso de la capa $K$ , en una muestra de composición $\{C_j\}$ irradiada durante un lapso $\Delta t$ con una corriente $i$ , el número de ionizaciones generadas en una capa aislada de espesor másico unitario puede calcularse a partir de la sección eficaz de ionización $Q_i$ como

$$n_i^o = i\Delta t Q_i(E_o) C_i \frac{N_o}{A_i} \omega_i f_i \frac{\Delta\Omega}{4\pi} \;,\rule[-0.8em]{0em}{1em}$$

La expresión (4) permite, en principio relacionar las intensidades características con las concentraciones $\{C_j\}$ incógnitas, aunque lo habitual es comparar estas intensidades con las $I_i^o$ correspondientes a un estándar

$$k_i \equiv \frac{I_i}{I_i^o} = \frac{C_i \int_0^\infty {\rm d}... ...}(\rho z) \phi_i^o(\rho z) e^{-\chi_i^o\rho z}} \;.\rule[-1.8em]{0em}{1em}$$

Esta razón es análoga a la $R_i$ definida en XRF; como en aquel caso, de este modo se evitan las imprecisiones inherentes a $Q_i$ , $\omega_i$ , $f_i$ o las transiciones Coster-Kronig, así como la dificultad de caracterizar el ángulo sólido $\Delta\Omega$ subtendido por el detector. Las matrices pueden ser similares como para que las integrales de esta expresión se cancelen; sin embargo, éste no es el caso general, ya que la dependencia de $k_i$ con la composición involucra a las posibles diferencias en las $\phi (\rho z)$ , así como en los $\chi$ (o, lo que es lo mismo, los $\mu$ ).

A las expresiones anteriores deben agregarse los reforzamientos por fluorescencia de otros elementos de la muestra, así como los correspondientes a fotones del espectro continuo. De este modo estaremos en condiciones de comparar nuestras predicciones con las razones de intensidades medidas. El factor de ``proporcionalidad'' entre $k_i$ y el cociente $C_i/C_i^o$ suele invocarse como correcciones por efectos de matriz, tradicionalmente llamadas correcciones ZAF. Al igual que en XRF, en primera aproximación puede proponerse que la razón de intensidades es muy parecida al cociente de concentraciones, al cual en este caso se le aplican tres factores de corrección

$$k_i = \frac{C_i}{C_i^o} \times {\cal Z A F} \;.$$

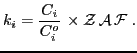
La corrección por efectos de matriz originalmente tenía en cuenta, en forma separada, tres efectos relacionados con la producción y el comportamiento de los rayos x diferentes en la muestra y en el estándar:
a) la generación de rayos x, puesto que hay diferencias en la sección eficaz de ionización, el poder de frenado y la dispersión de electrones (corrección $\cal Z$ );
b) la absorción de la radiación generada (corrección $\cal A$ );
c) el reforzamiento por fluorescencia secundaria (corrección $\cal F$ ).

A pesar de que se mantiene la costumbre de llamar `corrección ZAF' a los efectos de matriz, la mayoría de los modelos de corrección actualmente en vigencia evitan la separación de los factores $\cal Z$ y $\cal A$ . Esto se debe a que, además de que dicha separación es artificial, las aproximaciones se acumulan sin justificación, provocando desviaciones en los resultados mayores que los niveles deseados.

En nuestra notación, estas correcciones se expresan como

$${\cal Z} = \frac{\displaystyle\int_0^\infty {\rm d}(\rho z) \... ...\rho z}\mbox{\huge $/$}\int_0^\infty {\rm d}(\rho z) \phi_i^o(\rho z)} \;;$$

$${\cal F} = \frac{\displaystyle 1+\sum_j\frac{I_{ij}}{I_i^{(p)}}+ ... ... 1+\sum_j\frac{I_{ij}^o}{I_i^{o(p)}}+ \frac{I_{i,\rm cont}^o}{I_i^{o(p)}}} \;.$$

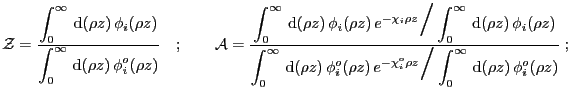
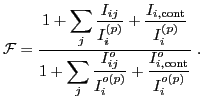
No se ha explicitado aquí la expresión correspondiente a la corrección $\cal F$ , que se torna particularmente complicada; se deja como ejercicio escribirla también en términos de $\phi\rho z)$ .

Siguiente: Partículas y muestras rugosas Subir: Microanálisis con sonda de Anterior: Distribución de ionizaciones