Siguiente: Red tridimensional monoatómica Subir: Cristal armónico clásico Anterior: Red unidimensional monoatómica
Supongamos ahora que contamos con dos iones iguales (de masa 







![$\displaystyle U = \frac{K}{2} \sum_n \left[ u_1\big(na\big)-u_2\big(na\big) \ri...
...+
\frac{G}{2} \sum_n \left[ u_2\big(na\big)-u_1\big((n+1)a\big) \right]^2 \;,
$](img824.svg)
![$\displaystyle \left\{ \begin{array}{l}
M\,\ddot{u}_1(na) = - \displaystyle \fr...
... \left[ u_2\big(na\big) - u_1\big((n+1)a\big) \right] \;.
\end{array} \right.
$](img825.svg)
 y
y
 diferentes
diferentes

![$\displaystyle \left\{ \begin{array}{rcr}
\left[M\omega^2-(K+G)\right] \epsilon...
...ft[M\omega^2-(K+G)\right] \epsilon_2 = 0
\rule{0em}{2em}
\end{array} \right.
$](img829.svg)
 no triviales debe
anularse el determinante del sistema de ecuaciones, es decir
no triviales debe
anularse el determinante del sistema de ecuaciones, es decir
![$\displaystyle \left[M\omega^2-(K+G)\right]^2 = \left\vert K+Ge^{-ika}\right\vert^2$](img831.svg) |
 |
|
 |
|
Reemplazando en las ecuaciones anteriores vemos que

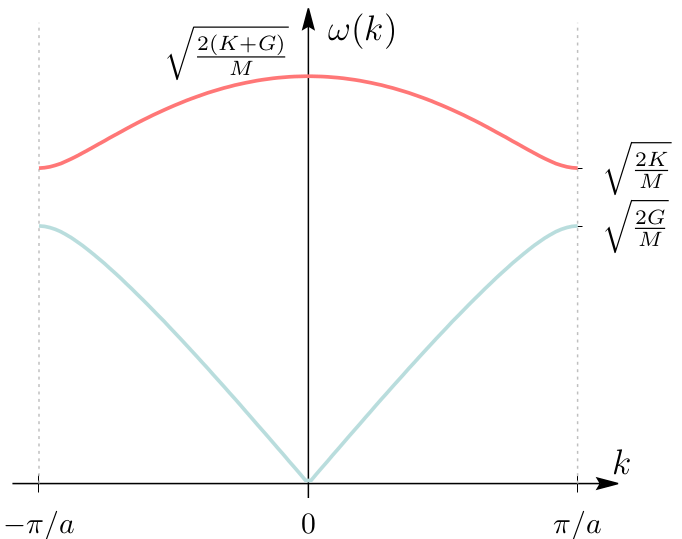
 , es decir , es decir  modos normales: la
relación de dispersión tiene 2 ramas. El comportamiento cualitativo de la rama
inferior es similar al de la red monoatómica: en particular para modos normales: la
relación de dispersión tiene 2 ramas. El comportamiento cualitativo de la rama
inferior es similar al de la red monoatómica: en particular para  se
cumple se
cumple
 , como sucede con las ondas de sonido, por lo cual se la
llama rama acústica. La rama superior se denomina rama óptica porque, como , como sucede con las ondas de sonido, por lo cual se la
llama rama acústica. La rama superior se denomina rama óptica porque, como
|
veremos en seguida, se asocia a la respuesta de los cristales a la
radiación electromagnética. La figura muestra las curvas para el caso en que

Analicemos el comportamiento de ambas ramas para 

 vale para la rama óptica y el
vale para la rama óptica y el  para la rama acústica: esto
significa que en este rango, los modos acústicos activan oscilaciones en fase en
los átomos de cada celda, mientras que las asociadas con los modos ópticos se
dan en oposición de fase. Justamente por este motivo se denomina rama óptica,
porque en el caso de cristales iónicos, la radiación electromagnética induce
desplazamientos opuestos en iones de signo contrario. En este límite entonces
para la rama acústica: esto
significa que en este rango, los modos acústicos activan oscilaciones en fase en
los átomos de cada celda, mientras que las asociadas con los modos ópticos se
dan en oposición de fase. Justamente por este motivo se denomina rama óptica,
porque en el caso de cristales iónicos, la radiación electromagnética induce
desplazamientos opuestos en iones de signo contrario. En este límite entonces

 , al igual que en las ondas acústicas.
, al igual que en las ondas acústicas.
Para 
 con
con
 con
con
 no se elongara).
no se elongara).
Si una de las interacciones es mucho más intensa que la otra, es decir si 
![$\displaystyle (K\gg G) \qquad \left\{ \begin{array}{l} \displaystyle
\omega_O ...
...] \;, \qquad
\epsilon_1\approx\epsilon_2 \rule{0em}{2em}
\end{array} \right.
$](img848.svg)
 es casi independiente de
es casi independiente de  , y se deja como ejercicio
mostrar que los desplazamientos se dan como si cada celda contuviera una
molécula aislada, con las dos masas unidas por el resorte oscilando siempre en
oposición de fase. La rama acústica en cambio se corresponde con una cadena
lineal de masa
, y se deja como ejercicio
mostrar que los desplazamientos se dan como si cada celda contuviera una
molécula aislada, con las dos masas unidas por el resorte oscilando siempre en
oposición de fase. La rama acústica en cambio se corresponde con una cadena
lineal de masa  , ya que se mueven en fase y siempre con igual amplitud (otro
ejercicio).
, ya que se mueven en fase y siempre con igual amplitud (otro
ejercicio).
Finalmente, cuando los valores de 


Gustavo Castellano 21/06/2023