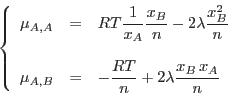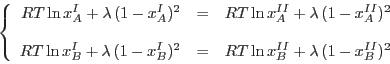Hemos visto que cuando un fluido consta de una mezcla de diferentes tipos de partículas puede ocurrir una separación del sistema en fases de diferente composición. El caso más sencillo es el de mezclas binarias, y cuando en una mezcla 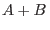 las partículas no interactúan entre sí (como en un gas ideal) el potencial de Gibbs total es
las partículas no interactúan entre sí (como en un gas ideal) el potencial de Gibbs total es
(como antes, el supraíndice 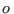 señala el potencial químico de una
sustancia pura). Si ahora suponemos que las partículas
señala el potencial químico de una
sustancia pura). Si ahora suponemos que las partículas 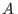 interactúan con
las
interactúan con
las 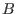 , debemos agregar a la energía interna un término proporcional al
número de pares
, debemos agregar a la energía interna un término proporcional al
número de pares 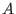 -
-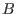 posibles:
posibles:
El denominador garantiza que este término también es extensivo. De esta
manera, el potencial de Gibbs molar resulta
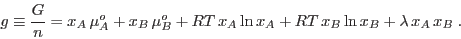 |
(10) |
Los sistemas binarios descriptos adecuadamente por esta relación se
denominan `regulares'. El parámetro 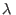 mide la magnitud de las
interacciones
mide la magnitud de las
interacciones 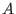 -
-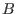 : si es positivo, las partículas
: si es positivo, las partículas 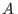 y
y 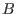 se
repelen, mientras que cuando es negativo, se atraen. Para el caso de
se
repelen, mientras que cuando es negativo, se atraen. Para el caso de
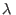 positivo y grande, a
positivo y grande, a 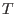 bajas la repulsión entre moléculas
``supera'' a la energía térmica, que tiende a mezclar las partículas y
homogeneizar el fluido. Por lo tanto el sistema puede separarse en dos
fases: una fase rica en
bajas la repulsión entre moléculas
``supera'' a la energía térmica, que tiende a mezclar las partículas y
homogeneizar el fluido. Por lo tanto el sistema puede separarse en dos
fases: una fase rica en 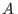 y otra rica en
y otra rica en 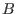 .
.
El potencial de Gibbs molar puede escribirse en términos de las tres
variables independientes 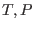 y
y 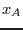 . Es posible entonces computar las
derivadas
. Es posible entonces computar las
derivadas
y
El último término del miembro de la derecha toma su valor mínimo (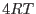 )
para
)
para 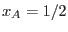 , de modo que
, de modo que
Es fácil ver que la condición de estabilidad significa que
para variaciones arbitrarias 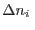 y
y 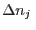 (en nuestro caso
(en nuestro caso
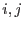 pueden valer
pueden valer 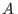 o
o 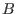 ); además,
); además,
De este modo, las cantidades
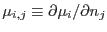 conforman una matriz simétrica definida positiva:
conforman una matriz simétrica definida positiva:
si la mezcla es estable.
Para procesos a 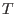 y
y 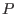 constantes, la relación de Gibbs-Duhem implica
constantes, la relación de Gibbs-Duhem implica
para
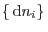 arbitrarios, de manera que debe cumplirse
arbitrarios, de manera que debe cumplirse
En nuestro caso esto se reduce a
de donde se deduce que
y análogamente 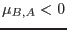 .
.
Por otro lado, de la ec. () podemos evaluar
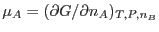 , teniendo presente que
, teniendo presente que
Así obtenemos
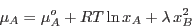 |
(11) |
y, análogamente,
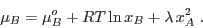 |
(12) |
De aquí resulta
Puede verse que la condición 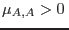 es equivalente a
es equivalente a 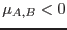 ,
y de ellas resulta que la condición de estabilidad local es
,
y de ellas resulta que la condición de estabilidad local es
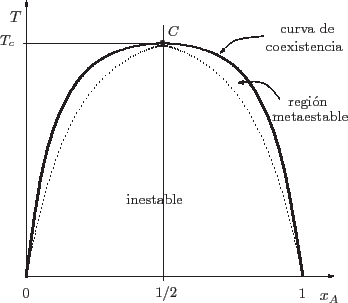
Esta condición se representa en la figura mediante la curva a trazos. A la
derecha de ella se tiene una fase rica en 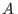 ( (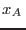 próximo a 1),
mientras que a la izquierda, una fase rica en próximo a 1),
mientras que a la izquierda, una fase rica en 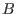 ( (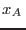 pequeño). En el
punto crítico pequeño). En el
punto crítico 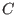 desaparecen las dos fases, y desaparecen las dos fases, y
pero
por lo que se recupera la condición de estabilidad.
Para cada 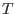 , la condición de coexistencia implica , la condición de coexistencia implica
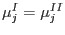 , de
manera que, de () y () obtenemos , de
manera que, de () y () obtenemos
|
|
Como la curva de coexistencia es simétrica respecto de 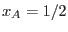 , allí se
cumple
, allí se
cumple
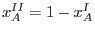 , de modo que la coexistencia estable se da para
, de modo que la coexistencia estable se da para
que es la curva continua de la figura. La región debajo de esta curva de
coexistencia es la zona en la que efectivamente hay coexistencia. La zona
metaestable es la comprendida entre las dos curvas: allí se satisface el
criterio de estabilidad local pero no global. El análisis del significado de
un punto debajo de la curva de coexistencia es idéntico al que realizamos en
los esquemas de coexistencia de las secciones anteriores.
Gustavo Castellano 12/06/2018
![]() las partículas no interactúan entre sí (como en un gas ideal) el potencial de Gibbs total es
las partículas no interactúan entre sí (como en un gas ideal) el potencial de Gibbs total es
![]() y
y ![]() . Es posible entonces computar las
derivadas
. Es posible entonces computar las
derivadas
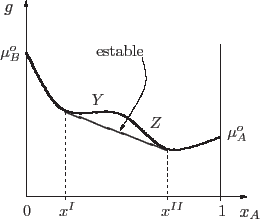
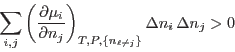
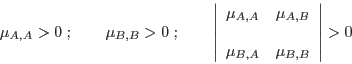
![]() y
y ![]() constantes, la relación de Gibbs-Duhem implica
constantes, la relación de Gibbs-Duhem implica
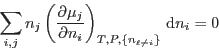
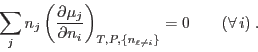
![]() , teniendo presente que
, teniendo presente que