Siguiente: Ferromagnetismo: Modelo de Ising Subir: Gas de Fermi-Dirac Anterior: Niveles de Landau
Analicemos ahora el comportamiento para temperaturas bajas. Como sabemos,
los electrones `intentan' ocupar los estados de energía más baja, aunque
también sabemos que a medida que se reduce el valor de ![]() ,
correspondientemente caben menos en el estado fundamental, porque la
degeneración
,
correspondientemente caben menos en el estado fundamental, porque la
degeneración ![]() disminuye linealmente con
disminuye linealmente con ![]() . Esto trae como
consecuencia oscilaciones en la magnetización, fenómeno que se conoce como
efecto de Haas - Van Alphen, a partir de los resultados de un famoso
experimento realizado por estos investigadores en 1930, en una muestra de
bismuto a 14,2 K entre 0,5 y 2 Tesla.
. Esto trae como
consecuencia oscilaciones en la magnetización, fenómeno que se conoce como
efecto de Haas - Van Alphen, a partir de los resultados de un famoso
experimento realizado por estos investigadores en 1930, en una muestra de
bismuto a 14,2 K entre 0,5 y 2 Tesla.
Al interesarnos en el caso
![]() , tomamos directamente
, tomamos directamente
![]() en las expresiones anteriores, e ignoramos el movimiento en la
dirección
en las expresiones anteriores, e ignoramos el movimiento en la
dirección ![]() , pues no aporta a la susceptibilidad magnética.
, pues no aporta a la susceptibilidad magnética.
Definiendo
![]() , los niveles de Landau pueden
escribirse como
, los niveles de Landau pueden
escribirse como
![]() , y en términos de
, y en términos de
![]() , donde
, donde ![]() es el número de partículas por unidad de área, su
degeneración es
es el número de partículas por unidad de área, su
degeneración es ![]() . La magnitud
. La magnitud ![]() representa el valor mínimo
para que todos los electrones quepan en cada uno de los niveles de Landau. A
representa el valor mínimo
para que todos los electrones quepan en cada uno de los niveles de Landau. A
![]() , cuando
, cuando ![]() todos los electrones se acomodan en el nivel
fundamental
todos los electrones se acomodan en el nivel
fundamental ![]() ; en ese caso, la energía por partícula será
; en ese caso, la energía por partícula será
![]() . Si en cambio
. Si en cambio ![]() , algunas partículas deben ocupar niveles más altos:
la condición para que los primeros
, algunas partículas deben ocupar niveles más altos:
la condición para que los primeros ![]() niveles de Landau (del 0 al
niveles de Landau (del 0 al ![]() )
estén ocupados completamente, el
)
estén ocupados completamente, el ![]() parcialmente lleno y los otros
vacíos es
parcialmente lleno y los otros
vacíos es
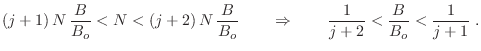
![$\displaystyle \frac{E_o}N = \frac{g}{N} \sum_{k=0}^j\epsilon_k +
\left[1-\frac...
...psilon_{j+1}
= \mu_o\,B\, \left[ 2j+3 - (j+1)(j+2)\,\frac{B}{B_o} \right] \;,
$](img1119.png)
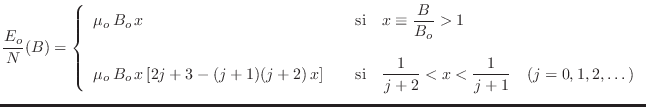
Puede obtenerse (¿cómo y por qué?) a partir de estas expresiones
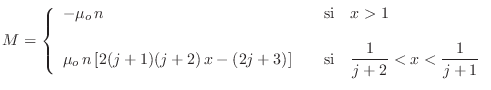
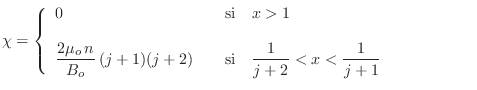
|
|
|
Gustavo Castellano 19/11/2021