Siguiente: Momento angular orbital Subir: clases-mc1 Anterior: Método WKB (Wentzel-Kramers-Brillouin)
Al igual que en la mecánica clásica, el momento angular reviste una gran importancia en la cuántica. Su conocimiento nos permite también en esta área aprovechar las ventajas que ofrecen problemas con simetrías de rotación, que justamente aparecen en sistemas moleculares, atómicos y nucleares.
A partir del principio de correspondencia, el momento angular orbital para una partícula queda definido por



![$\displaystyle [\hat{L}_j,\hat{L}_k]=i\hbar\,\varepsilon_{jk\ell}\,\hat{L}_\ell\...
...ell\;, \qquad
[\hat{L}_j,\hat{p}_k]=i\hbar\,\varepsilon_{jk\ell}\,\hat{p}_\ell$](img1066.svg) (ejercicio).
(ejercicio).
Las relaciones anteriores deben ser válidas para cualquier momento angular



 ,
,
 y
y
 no conmutan entre sí, por lo cual no pueden diagonalizarse simultáneamente. En cambio el operador escalar
no conmutan entre sí, por lo cual no pueden diagonalizarse simultáneamente. En cambio el operador escalar

![$\displaystyle [\hat{J}^2,\hat{J}_k]=0 \qquad (k=x,y,z) \;.
$](img1073.svg)
 y alguna de las componentes
y alguna de las componentes
 ; por convención, elegimos
; por convención, elegimos
 . Identificamos los autovalores de
. Identificamos los autovalores de
 con el parámetro
con el parámetro  , mientras que para los de
, mientras que para los de
 utilizamos
utilizamos  ; entonces señalamos como
; entonces señalamos como
 los estados cuánticos de un sistema —con respecto a estos dos operadores. Podemos escribir las correspondientes ecuaciones de autovalores como
los estados cuánticos de un sistema —con respecto a estos dos operadores. Podemos escribir las correspondientes ecuaciones de autovalores como

 y
y  se introducen por comodidad, de manera que
se introducen por comodidad, de manera que  y
y  sean adimensionales. Como siempre, tomamos los estados
sean adimensionales. Como siempre, tomamos los estados
 ortonormales:
ortonormales:

La simetría de las relaciones de conmutación sugiere introducir —de manera semejante al desarrollo para el oscilador armónico— los operadores




Resulta directo mostrar las relaciones (ejercicio)
![$\displaystyle [\hat{J}^2,\hat{J}_\pm] = 0 \;,\qquad
[\hat{J}_+,\hat{J}_-] = 2\hbar\,\hat{J}_z \;,
\qquad [\hat{J}_z,\hat{J}_\pm] = \pm\hbar\,\hat{J}_\pm \;,
$](img1086.svg)
 |
|||
 |
 |

 sobre los autovectores
sobre los autovectores
 . Por ejemplo, si aplicamos
. Por ejemplo, si aplicamos
 sobre el ket
sobre el ket
 ,
,

 es también autoestado de
es también autoestado de
 , con autovalor
, con autovalor
 . Análogamente
. Análogamente

 no afecta el número cuántico
no afecta el número cuántico  . Podemos resumir estas dos condiciones como
donde
. Podemos resumir estas dos condiciones como
donde
 es una constante de normalización.
es una constante de normalización.
A partir de estos resultados pueden inferirse varias conclusiones acerca de los autovalores 







 para el cual
para el cual
 =0, porque no puede seguir subiendo el valor de
=0, porque no puede seguir subiendo el valor de  . Esto significa que al aplicar
. Esto significa que al aplicar
 sobre
sobre
 tendremos
tendremos


Un razonamiento similar nos conduce a que habrá una cota inferior






 a
a
 en algún momento habremos llegado al mínimo valor
en algún momento habremos llegado al mínimo valor
 ; llamando
; llamando  al número de veces que es necesaria esta operación, relacionamos ambos valores extremos
al número de veces que es necesaria esta operación, relacionamos ambos valores extremos


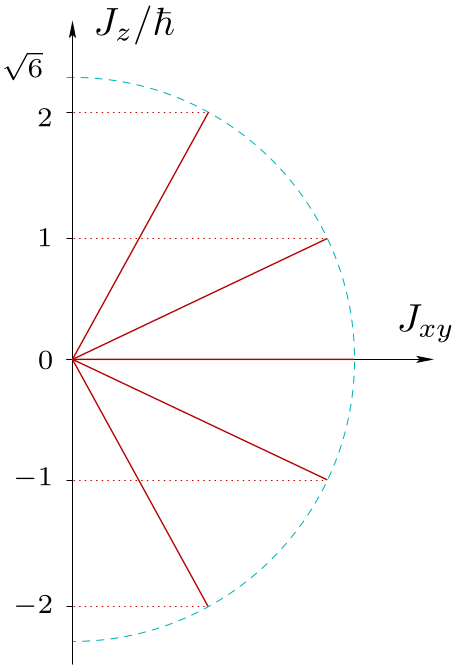
 será entonces un número entero o semientero (no negativo, recuérdalo). Sintetizando,
será entonces un número entero o semientero (no negativo, recuérdalo). Sintetizando,
 y
y
 )
)
![$\displaystyle \fbox{\ \ $\hat{J}^2 \vert j,m\rangle = \hbar^2\,j\,(j+1)\,\vert ...
...-j \le m \le j\quad \mbox{(entero o semientero)}.
\rule[-1.2em]{0em}{3em} $ }
$](img1120.svg)
Volviendo a la relación (30), que ahora escribimos



 ,
,
![$\displaystyle \vert C_{jm}^+\vert^2=\langle j,m\vert\hat{J}_-\hat{J}_+\vert j,m...
...+1)]
\qquad \Rightarrow \qquad C_{jm}^+ = \hbar\,\sqrt{j\,(j+1)-m\,(m+1)} \;,
$](img1125.svg)
 encontramos
encontramos

 sobre
sobre
 se resume entonces como
o bien
se resume entonces como
o bien

Esto nos permite a su vez evaluar los valores de expectación para las componentes


![$\displaystyle \hat{J}_x\vert j,m\rangle = \frac{1}{2} \left(\hat{J}_++\hat{J}_-...
...j+m+1)}\,\vert j,m+1\rangle +
\sqrt{(j+m)(j-m+1)}\,\vert j,m-1\rangle \right] ,$](img1131.svg) |
|||
![$\displaystyle \hat{J}_y\vert j,m\rangle = \frac{1}{2i} \left(\hat{J}_+-\hat{J}_...
...,m+1\rangle -
\sqrt{(j+m)(j-m+1)}\,\vert j,m-1\rangle \right] . \rule{0em}{2em}$](img1132.svg) |
 conforman una base ortonormal, en cualquier estado
conforman una base ortonormal, en cualquier estado
 se cumple entonces
se cumple entonces

 y
y
 (sus autovectores), las componentes
(sus autovectores), las componentes
 y
y
 están absolutamente indeterminadas. En virtud de que los
están absolutamente indeterminadas. En virtud de que los
 son autoestados de
son autoestados de
 y
y
 sabemos que los valores de expectación para el módulo de
sabemos que los valores de expectación para el módulo de
 y
y
 son
son
|
|
|