Potencial periódico débil (mezclado con el texto de Dresselhaus)

Si el potencial $U$ se anula, la ecuación de Schrödinger es la de la partícula libre, y las soluciones son ondas planas que solo deben respetar la periodicidad macroscópica de nuestro sistema, y las autoenergías son

$$\varepsilon^o(\bm{k}) = \frac{\hbar^2k^2}{2m} \;.$$

Cuando el potencial $U(\bm{r})\!\neq\!0$ no altera demasiado las autoenergías individuales ni las soluciones de ondas planas $\psi_{\bm{k}}^o(\bm{r})\!=\!(1/\sqrt{V})e^{i\bm{k}\cdot\bm{r}}$ (o $\left\vert \bm{k} \right\rangle$ en la notación de Dirac), entonces es posible encarar el problema considerando a $U(\bm{r})$ como una perturbación independiente del tiempo. En este contexto, estimamos las autoenergías mediante las correcciones

$$\varepsilon(\bm{k}) = \varepsilon^o(\bm{k}) + {\color{gray}\unde... ...\right\rangle \right\vert^2}{\varepsilon^o(\bm{k})-\varepsilon^o(\bm{k'})} \;.$$

Es directo verificar que la corrección de primer orden resulta proporcional al coeficiente $U_{\bm{0}}$, que se anula en virtud de nuestra elección para el cero de las energías⁶. Entonces es necesario tener en cuenta las correcciones de segundo orden, para lo cual expresamos los elementos de matriz como

$$\left\langle \bm{k} \right\vert U\left\vert \bm{k'} \right\rangle... ...\frac{1}{V} \int_V \,{\rm d}^3\bm{r}\; e^{i\,\bm{q}\cdot\bm{r}}\,U(\bm{r}) \;,$$

donde sustituimos $\bm{q}\!=\!\bm{k'}\!-\!\bm{k}$. Como $\bm{r}$ recorre todo el volumen $V$ del sólido, puede representarse como un vector $\bm{r'}$ dentro de una celda primitiva trasladado hasta $\bm{r}$ mediante un vector $\bm{R}_{\bm{n}}$ ( $\bm{n}\!=\!(n_1,n_2,n_3)$ enteros) de la red de Bravais, es decir $\bm{r}\!=\!\bm{r'}\!+\!\bm{R}_{\bm{n}}$. La integral anterior puede entonces realizarse acumulando las integrales correspondientes a cada celda unidad de volumen $v\!=\!V/N$, y teniendo presente que el período del potencial es el de la red,

$$\left\langle \bm{k} \right\vert U\left\vert \bm{k'} \right\rangle... ...\right) \int_v \,{\rm d}^3\bm{r'}\; e^{i\,\bm{q}\cdot\bm{r'}}\,U(\bm{r'}) \;,$$

En términos de los vectores primitivos $\{\bm{a}_{\ell}\}$ y $\{\bm{b}_j\}$ de la red directa y recíproca, respectivamente, expresamos $\bm{R}_{\bm{n}}\!=\!\sum_{\ell=1}^{3}n_{\ell}\bm{a}_{\ell}\,$ y $\,\bm{q}\!=\!\sum_{j=1}^{3}\alpha_j\bm{b}_j\,$; en particular, recordemos que se satisface (7), es decir $\alpha_j\!=\!m_j/N_j\,$, con $m_j\in\mathbb{Z}$. Teniendo presente que se cumple $\,\bm{a}_{\ell}\!\cdot\!\bm{b}_j\!=\!2\pi\,\delta_{\ell j}\,$, la suma entre paréntesis puede resolverse exactamente (ejercicio)

$$\sum_{{\bm{n}}=(1,1,1)}^{N_1,N_2,N_3} e^{i\,\bm{q}\cdot\bm{R}_{\b... ..._{j=1}^{3} \left[ \frac{1-e^{i\,2\pi\,m_j}}{e^{-i\,2\pi\,m_j/N_j}-1} \right]}.$$

La última igualdad vale siempre que $e^{i\,2\pi\,\alpha_j}\!=\!e^{i\,2\pi\,m_j/N_j}\!\neq\!1\,$: en ese caso, la sumatoria se anula (porque $m_j$ es entero), y por lo tanto tampoco hay corrección de segundo orden en las energías. Sin embargo, cuando los $\alpha_j\!=\!m_j/N_j\,$ son enteros todos los términos dentro del corchete aportan con 1 unidad, y el producto de las sumas parciales es $N_1N_2N_3\!=\!N$. Esa situación se da cuando $\bm{q}\!=\!\bm{k'}\!-\!\bm{k}\!=\!\sum_{j=1}^{3}\alpha_j\bm{b}_j\,$ coincide entonces con un vector $\bm{G}$ de la red recíproca. El elemento de matriz que buscábamos resulta

$$\left\langle \bm{k} \right\vert U\left\vert \bm{k'} \right\rangle... ...{\bm{k'}\!-\bm{k},\bm{G}} = U_{\bm{G}}\; \delta_{\bm{k}-\bm{k'}\!,\bm{G}} \;,$$

donde en la última expresión cambiamos el signo de $\bm{k'}\!-\!\bm{k}$, según la definición (8) de $U_{\bm{G}}\,$. Resumiendo, la teoría de perturbaciones nos permite afirmar que las energías $\varepsilon(\bm{k})$ son muy parecidas a las de los electrones libres cuando los estados representados por $\bm{k}$ no están conectados con otro $\bm{k'}$ mediante un desplazamiento por un vector de la red recíproca —por supuesto, siempre dentro de la primera zona de Brillouin, ya que todos los estados $\bm{k}$ se corresponden con cualquier otro $\bm{k'}\!=\bm{k}-\bm{G}$, fuera de la PZB. Sin embargo, cuando nos aproximamos al borde de la PZB, el denominador de la expresión anterior se anula, y justamente el momento cristalino se corresponde con el de otro extremo de la celda primitiva del espacio recíproco. Entonces la expresión

$$\varepsilon(\bm{k}) = \varepsilon^o(\bm{k}) + \frac{2m}{\hbar^2} ... ...m}}} \frac{\left\vert U_{\bm{G}}\right\vert^2}{k^2-{\vert\bm{k}-\bm{G}\vert}^2}$$ (11)

nos indica dos cosas importantes: por un lado, que cuando se cumple la condición de Laue  $k^2={\vert\bm{k}-\bm{G}\vert}^2$, el denominador del último término se anula; por el otro, que cuando eso ocurre las correspondientes autoenergías son idénticas, es decir hay degeneración y debemos retomar los cálculos mediante la teoría de perturbaciones apropiada.

Así, una vez que identificamos los momentos cristalinos de la PZB que son equivalentes (idéntica autoenergía), recordemos que debemos efectuar un cambio de base para diagonalizar la matriz asociada con la perturbación (construida con los elementos $\left\langle \bm{k} \right\vert U\left\vert \bm{k}\!-\!\bm{G} \right\rangle$) en el subespacio asociado a la degeneración, lo que nos lleva a correcciones a $\varepsilon(\bm{k})$ en primer orden en la nueva base, que típicamente levantan la degeneración⁷. Por ejemplo, si solo hay un $\bm{G}_1$ que conecta dos estados de la PZB, es decir $\bm{k}_1$ y $\bm{k}_1\!-\!\bm{G}_1$, necesitamos resolver

$$\left\vert \begin{array}{ccc} \varepsilon^o(\bm{k}) + \textcolor{... ...1)}(\bm{k}\!-\!\bm{G}_1)} - \varepsilon \\ \par \end{array}\right\vert = 0 \;.$$ (12)

Aquí debe tenerse en cuenta que las correcciones de primer orden $\varepsilon^{(1)}$ en la base $\{\left\vert \bm{k} \right\rangle \}$ se anulan, y que en realidad, para $\bm{k}\!=\!\bm{k}_1$, $\varepsilon^o(\bm{k}_1\!-\!\bm{G}_1)\!=\!\varepsilon^o(\bm{k}_1)$. Todo esto puede verse también volviendo a la ec. (9)

$$\left(\frac{\hbar^2k^2}{2m} - \varepsilon\right) c_{\bm{k}} + \sum_{\bm{G}}U_{\bm{G}}\,c_{\bm{k}-\bm{G}} = 0 \;,$$

y considerando en el ejemplo previo un único estado con $\bm{G}\!=\!+\bm{G}_1$ conectado con el $\bm{k}\!=\!\bm{k}_1$ de interés (un solo sumando), vinculado con otra ecuación que involucra a $\bm{k}\!=\!\bm{k}_1\!-\!\bm{G}_1$ con un único término $\bm{G}\!=\!-\bm{G}_1$ en la sumatoria: tendrá solución no trivial el sistema de ecuaciones resultante para $c_{\bm{k}_1}$ y $c_{\bm{k}_1\!-\!\bm{G}_1}$

$$\left\{ \begin{array}{cccl} \displaystyle\left(\frac{\hbar^2 k_1^... ...\!}{2m} - \varepsilon\right) c_{\bm{k}_1\!-\!\bm{G}_1} &= 0 \end{array} \right.$$ (13)

cuando se cumpla la condición (12) anterior, teniendo en cuenta que (ejercicio) $\left\langle \bm{k}\!-\!\bm{G}_1 \right\vert U\left\vert \bm{k} \right\rangle \!=\!U_{-\bm{G}_1}\!=\!\left(U_{\bm{G}_1}\right)^*$.

Resolviendo entonces el determinante (12) obtenemos

$$\left(\varepsilon-\varepsilon^o(\bm{k})\right) \left(\varepsilon-\varepsilon^o(\bm{k}\!-\!\bm{G}_1)\right) = \left\vert U_{\bm{G}_1}\right\vert^2$$ (14)

$$\quad\Rightarrow\quad \varepsilon = \frac{\varepsilon^o(\bm{k})+\varepsilon^o(\bm{k}\!-\!\bm{G}_1)}{2... ...varepsilon^o(\bm{k}\!-\!\bm{G}_1)}{2}\right]^2 + \vert U_{\bm{G}_1}\vert^2} \;,$$

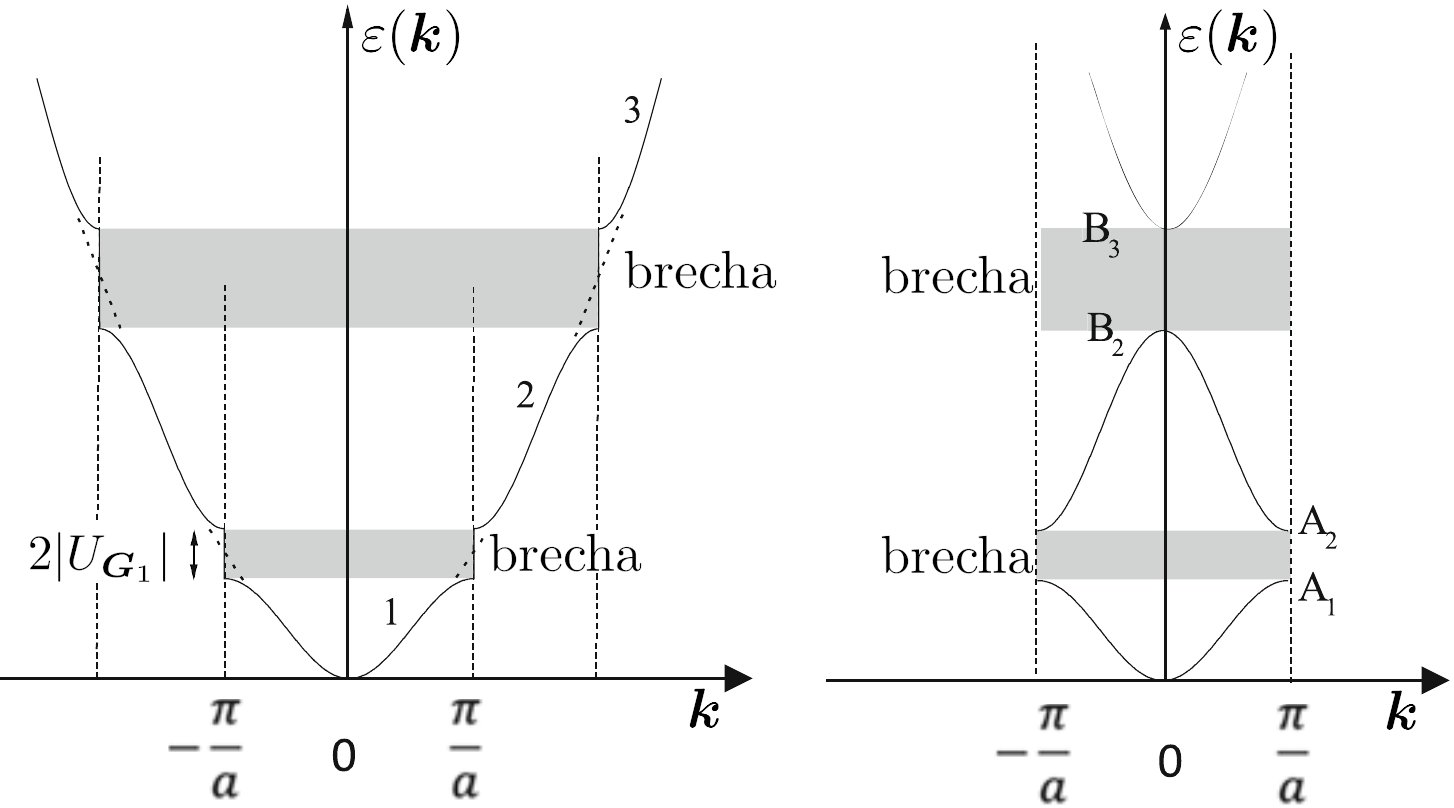
En particular, cuando se cumple la condición de Laue mencionada arriba, es decir cuando el vector $\bm{k}$ alcanza exactamente el plano de Bragg, $$\varepsilon(\bm{k}_1) = \varepsilon^o(\bm{k}_1) \pm \vert U_{\bm{G}_1}\vert \;,$$ con lo cual las energías que para la partícula libre con $\bm{k}\!=\!\bm{k}_1$ valían $\hbar^2 k_1^2/(2m)$, ahora pasan a separarse $2\vert U_{\bm{G}_1}\vert$. Además, de la (14) vemos que $$\left.\frac{\partial\varepsilon}{\partial\bm{k}}\right\vert _{\bm{k}=\bm{k}_1} = \frac{\hbar^2}{m}\left(\bm{k}_1-\frac{\bm{G}_1}{2}\right) \;,$$ es decir, $\nabla_{\bm{k}}\varepsilon$ es paralelo al plano de Bragg: las superficies de $\varepsilon$ constante son perpendiculares al plano de

 

Bragg. Para estos casos, si volvemos a la (13) en la situación de $U_{\bm{G}_1}$ real ($U(\bm{r})$ par), concluimos que $c_{\bm{k}_1}\!=\!\pm \sgn (U_{\bm{G}_1})\,c_{\bm{k}_1\!-\!\bm{G}_1}\,$. Entonces, cuando $U_{\bm{G}_1}>0$

 

$$\hspace{20em} \left\{ \begin{array}{ll} \vert\psi(\bm{r})\vert^2 ... ...on^o(\bm{k}_1) - \vert U_{\bm{G}_1}\vert \;,\rule{0em}{2em} \end{array} \right.$$

mientras que cuando $U_{\bm{G}_1}<0$

 

$$\hspace{20em} \left\{ \begin{array}{ll} \vert\psi(\bm{r})\vert^2 ... ...on^o(\bm{k}_1) - \vert U_{\bm{G}_1}\vert \;.\rule{0em}{2em} \end{array} \right.$$

La obtención de estas estructuras para un problema unidimensional de parámetro $a$ es bastante sencilla, como ocurre con el potencial $U(x)=-V_o\cos(2\pi\,x/a)$ (ejercicio), que puede extenderse fácilmente a una sumatoria de términos similares, siempre respetando la periodicidad de la red (con múltiplos de $2\pi/a$).

Para estructuras en 2 o 3 dimensiones, el problema se complica principalmente al momento de encontrar en qué casos se dan las degeneraciones: el desafío es hallar los $\bm{G}$ que intervienen en la sumatoria del miembro de la izquierda de (11), ya que el resto del desarrollo es similar al presentado para el caso en que contribuye un único término. Lo habitual es proveer la descripción a lo largo de una curva definida entre puntos de alta simetría del sistema: en cada tramo se da una parametrización y se traza una curva como en un sistema unidimensional.