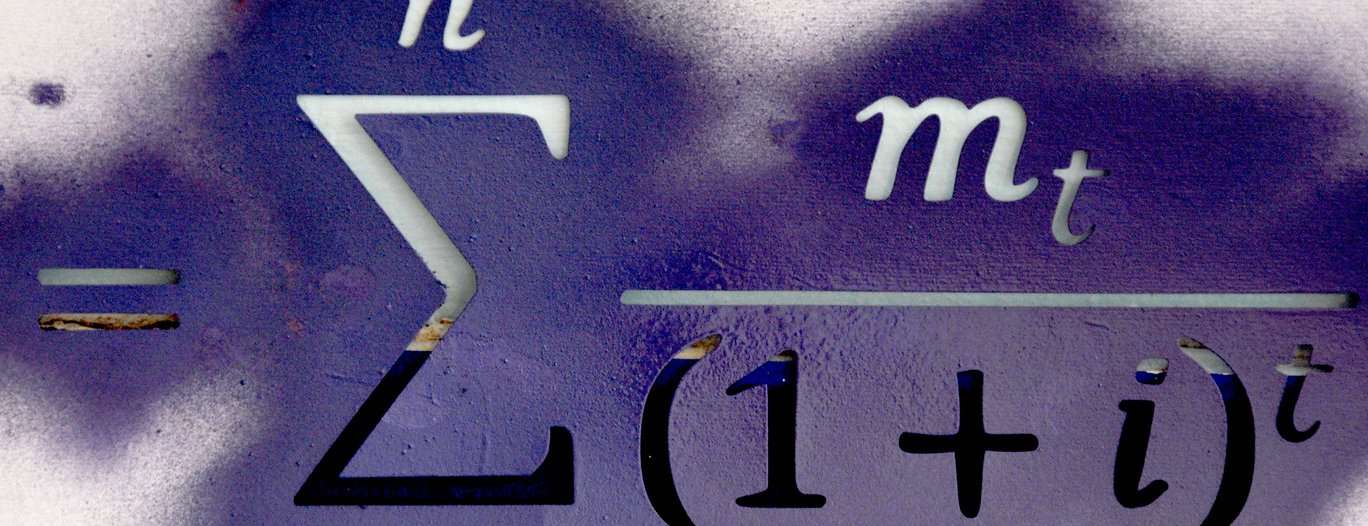
Profesorado en Matemática
- Duración de la carrera: 4 años
- Requisitos de Admisión: ver Admisión
- Ver Video Institucional: Click aquí
- Régimen de CorrelatividadesClick aquí
La formación recibida posibilita a los egresados una salida laboral amplia, ya que pueden ser docentes en el nivel medio como también en Institutos de Formación Docente. Pudiendo intervenir, en este último caso, tanto en la formación de Profesores/as de Matemática como de Profesores/as de Nivel Primario o Inicial, en áreas disciplinares o vinculadas con la Educación Matemática. Algunos/as de los/as egresados/as de la institución han accedido también a cargos en universidades públicas o privadas.
Uno de los aportes de los profesores en Matemática será mostrar que el conocimiento es el resultado de un largo proceso; y que la ciencia es una actividad tendiente al enriquecimiento de este conocimiento y a la obtención de un mayor bienestar en armonía con el medio que lo rodea.
A partir de los conocimientos teóricos y prácticos adquiridos en los diferentes espacios curriculares, podrá identificar problemas educacionales y así implementar, en su propio lugar de trabajo, las estrategias que influirán en modificaciones de práctica educativas acordes a las necesidades locales y teniendo en cuenta tendencias actuales en la educación matemática.
El diploma que acredita la carrera de grado universitario y la formación recibida posibilita también a los egresados seguir carreras de postgrado y dedicarse a la investigación de problemáticas vinculadas con la enseñanza y el aprendizaje de la Matemática en diferentes niveles educativos.
Febrero
1º año
Contenido mínimo
Cálculo algebraico. Teoría de conjuntos y lógica. Funciones. Trigonometría.
1º año
1º año primer cuatrimestre
Contenido mínimo
[-] Relaciones y funciones. [-] Números naturales. Principio de inducción. Principio de buena ordenación. [-] Combinatorias. Problemas de conteo. Binomio de Newton.. [-] Números entero. Divisibilidad. Desarrollos s-ádicos. Máximo común divisor y mínimo común múltiplo. Algoritmo de Euclides. Números primos. Teorema fundamental de la aritmética. [-] Congruencias. Ecuaciones lineales en congruencia. Congruencias simultáneas. Aritmética módulo n. Teorema pequeño de Fermat. [-] Números complejos. Propiedades fundamentales. Conjugados. Valor absoluto. Fórmula de Moivre. Raíces n-ésimas de un número complejo. [-] Grafos no orientados. Valencia. Ciclos. Caminos y caminatas.
1º año primer cuatrimestre
Contenido mínimo
Números reales. Propiedades. Supremo e ínfimo. Valor absoluto. Funciones. Gráficos. Funciones trigonométricas. Límites. Límites notables. Asíntotas verticales y horizontales. Funciones continuas. Teorema del valor intermedio. Valores extremos de funciones continuas en intervalos cerrados. Derivadas. Reglas de la derivación. Extremos relativos. Teorema de Rolle, del valor medio y del valor medio de Cauchy. Regla de L´Hopital. Derivadas sucesivas. Aplicaciones al esbozo de gráficos de funciones. Derivadas de funciones inversas. Nociones de antiderivadas.
1º año segundo cuatrimestr
Contenido mínimo
Integral definida. Teoremas fundamentales del Cálculo. Diferenciación e integración. Áreas, volúmenes, longitudes. Funciones Exponencial y Logarítmica. Métodos de integración por sustitución y partes. Integración de funciones racionales. Integral impropia. Teorema de Taylor y estimación del resto. Sucesiones y series numéricas. Series de potencias. Series de Taylor.
1º año segundo cuatrimestr
Contenido mínimo
Resolución de ecuaciones lineales. Matrices. Operaciones elementales. Matriz inversa. Espacios vectoriales sobre R y C. Subespacios. Independencia lineal. Bases y dimensión. Rectas y planos en Rn. Transformaciones lineales y matrices. Isomorfismos. Cambio de bases. Núcleo e imagen de transformaciones lineales. Rango fila y columna. Determinante de una matriz. Cálculo y propiedades básicas. Espacios con producto interno. Desigualdad de Cauchy-Schwartz. Desigualdad triangular. Teorema de Pitágoras. Ortonormalización de Gram-Schmidt. Ecuaciones de rectas y planos en Rn. Distancias. Introducción a vectores y valores propios. Aplicaciones. Diagonalización de matrices simétricas.
2º año
2º año primer cuatrimestre
Contenido mínimo
Autovalores. Autovectores. Teorema de Cayley-Hamilton. Operadores simétricos. Diagonalización. Aplicaciones geométricas. Cuádricas y cónicas.
2º año primer cuatrimestre
Contenido mínimo
Funciones vectoriales. Funciones de una variable. Longitud de arco. Límites y continuidad. Integrales de línea. Derivadas parciales. Derivadas parciales vectoriales. Funciones diferenciables y diferencial. Matriz Jacobiana. Diferenciabilidad de las funciones con derivadas parciales continuas. Derivadas direccionales. Gradiente. Función potencial. Regla de la cadena. Ecuaciones en derivadas parciales (ejemplos). Teorema de la función inversa e implícita. Valores extremos. Multiplicadores de Lagrange. Desarrollos en series de Taylor y valores extremos. Integrales múltiples en R2 y R3. Cambio de variables. Coordenadas esféricas y cilíndricas. Teorema de Green, Gauss y Stokes. Aplicaciones.
2º año primer cuatrimestre
Contenido mínimo
2º año segundo cuatrimestr
Contenido mínimo
Estudio de las ecuaciones de movimiento de una partícula. Sistemas de muchas partículas. Leyes de conservación de la energía en la mecánia. Experiencias de laboratorio. El campo electromagnético y gravitatorio.
2º año segundo cuatrimestr
Contenido mínimo
2º año segundo cuatrimestr
Contenido mínimo
El sistema axiomático de la geometría del plano según Euclides-Hilbert: [-] Axiomas Incidencia y Orden. [-] Axiomas de Congruencia. [-] Simetrías centrales y axiales, mediatrices y bisectrices. [-] Triángulos. [-] Intersección de Circunferencias (entre sí) y Rectas. [-] Paralelismo. [-] Clasificación de las transformaciones rígidas. [-] Construcciones con regla y compás.
3º año
3º año anual
Contenido mínimo
Didáctica de la matemática: campo de estudio. Tendencias actuales en educación matemática. La metodología de resolución de problemas: Polya, Schoenfeld, etc. El constructivismo y el constructivismo radical. La teoría didáctica de la mtemática francesa. Análisis de tetos y observación de clases. Reflexiones de prácticas docentes.
3º año primer cuatrimestre
Contenido mínimo
Geometría analítica de las secciones cónicas. Transformaciones del plano y del espacio euclídeo. Grupos de transformaciones rígidas, de semejanzas y de afinidades.
3º año primer cuatrimestre
Contenido mínimo
Mínimos elementos de programación necesarios para el manejo de paquetes específicos. Estudio de funciones a partir de su gráfico. Algoritmos para resolver ecuaciones no lineales. Algoritmos para encontrar soluciones de sistemas de ecuaciones lineales. Fórmulas de integración numérica. Empleo de software de uso libre aptos para funcionar en distintos sistemas operativos.
3º año segundo cuatrimestr
Contenido mínimo
Definciones básicas en la teoría de probabilidades para espacios mustrales físicos. Estadístrica descriptiva e inferencial Técnicas de estadístricas paramétricas y no paramétricas.
3º año segundo cuatrimestr
Contenido mínimo
Números, regiones y funciones complejas. Funciones holomorfas. Funciones exponenciales y trigonométricas. Funciones armónicas. Aplicaciones conformes.
4º año
4º año anual
Contenido mínimo
Observación de la realidad: institucional y áulica. La institución escolar: sus dimensiones. La organización práctica: Aspectos pedagógicos-didácticos. Rol docente y alumno. El proyecto de práctica. Elaboración, fundamentación, desarrollo y evaluación. Práctica en niveles secundarios y terciarios del sistema. Adecuación de proyectos didácticos. Análisis de la práctica. El docente y la reflexión crítica.
4º año anual
Contenido mínimo
El conocimiento Matemático y Fisico y la práctica docente. Un análisis reflexivo. La formación permanente del docente de ciencias y los problemas del pensamiento del profesor, las concepciones docentes y los conocimientos previos. Investigaciones con Didáctica de la Matemática y de la Física, relación con el profesorado. El curriculum de ciencias y su relación con los diferentes niveles del sistema. Relación Ciencia-Técnica-Sociedad. Actitudes hacia las Ciencias.
4º año primer cuatrimestre
Contenido mínimo
Nociones de espacios métricos y topológicos. Continuidad. Conexión y compacidad.
4º año primer cuatrimestre
Contenido mínimo
Medida exterior en Rn . Medida de Lebesgue. Funciones medibles. Integral de Lebesgue. Propiedades.
4º año
Contenido mínimo
Planteo de la dinámica newtoniana usando cálculo vectorial. Elementos de elasticidad e hidrostática. Formulación Lagrangiana y Hamiltoniana de la mecánica. Elementos de elasticidad, hidrostática y cinemática relativista.
4º año
Contenido mínimo
Valor temporal del dinero. Mercados financieros y productos financieros derivados. Valoración por arbitraje y técnicas de cobertura dinámica. Cálculo estocástico aplicado a finanzas. Martingalas. Números y cambios de medida. Movimientos browniano. Cálculo de lto. Modelado de precios de activos. El modelo binomial. El modelo de Black Sholes. Valoración neutral de riesgo. Fórmulas de Black Sholes. Volatilidad implícita. Modelos de tasas de interés. Estructuras a término. Tasas forward. Modelos de tasa corta.
4º año
Contenido mínimo
Estructuras ordenadas: reticulados y álgebras de Boole. Sistemas formales. Introducción a la lógica proposicional: enfoque sintáctico y semántico. Técnicas de pruebas. Estructura de las pruebas formales: deducción natural. Lenguajes formales y autómatas. Minimización de autómatas. Expresiones regulares. Gramáticas libres de contexto. Jerarquía de Chomsky. Gramáticas e isomorfismos.
4º año
Contenido mínimo
Curvas en ℝ³. Curvatura y torsión. Curvatura signada de curvas planas. Ecuaciones de Frenet. Teorema fundamental de la teoría local de curvas. Superficies en ℝ³. Superficies de nivel. Isometrías de ℝ³.. Primera forma fundamental. Superficies congruentes. Superficies isométricas y localmente isométricas. Conexión. Superficies orientadas. Aplicación normal de Gauss. Segunda forma fundamental. Curvatura normal de una curva regular en una superficie. Área de superficies parametrizadas. Geodésicas.